Calculation of magnetic dipole moment of the Earth

These calculations are from these notes from MIT OCW's 8.02 "Electromagnetism", on page 27.

We can represent the location of a point ##P## on the surface of the Earth using spherical coordinates

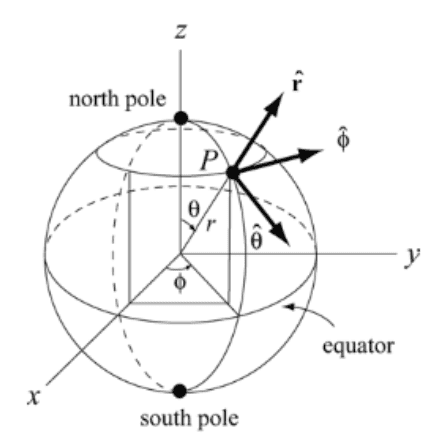
Let the ##z##-axis be the Earth's rotation axis, and the ##x##-axis passes through the prime meridian (that is, the constant zero longitude line passing through Greenwich, UK). Note that the ##x##-axis passes through the equator not Greenwich.

The corresponding magnetic dipole moment of the Earth can be written



Where did these specific angles and also ##\mu_E## come from?

The angles could be just an arbitrary example. Compare with the ensuing text where they use the location of MIT.

Here is the context of the calculations in the OP.

In this previous question I show a calculation of the magnetic field for a general point ##P## due to a current ring.

Setting up the coordinate system such that ##P## is in the ##yz##-plane, and under the assumption that point ##P## is very far away from the current ring, we reach the conclusion that

$$B_y=\frac{\mu_0}{4\pi}\frac{3\mu\sin{\theta}\cos{\theta}}{4^3}$$

$$B_z=\frac{\mu_0}{4\pi}\frac{\mu}{4^3}(3\cos^2{\theta}-1)$$

where ##\vec{\mu}=\mu\hat{k}## is the magnetic dipole moment, ##r## is the distance to ##P##, and ##\theta## is the spherical coordinates Azimuthal angle.

These equations describe a dipole field.

Next, let's obtain the magnetic field at this far away point ##P## in terms of the spherical coordinate vectors ##\hat{r}## and ##\hat{\theta}##.

The calculations result in

$$\vec{B}=(B_y\sin{\theta}+B_z\cos{\theta})\hat{r}+(B_y\cos{\theta}-B\sin{\theta})\hat{\theta}$$

and subbing in ##B_y## and ##B_z## we obtain

$$\vec{B}=-\frac{\mu_0}{4\pi}\frac{\mu}{r^3}(2\cos{\theta}\hat{r}+\sin{\theta}\hat{\theta})$$

$$=\frac{\mu_0}{4\pi}\frac{3(\vec{\mu}\cdot\hat{r})\hat{r}-\vec{\mu}}{r^3}$$

At this point, the exposition on the magnetic dipole moment of the Earth is shown.

I have no idea where the equation

$$\vec{\mu}_E=\mu_E(\sin{\theta_0}\cos{\phi_0}\hat{i}+\sin{\theta_0}\sin{\phi_0}\hat{j}+\cos{\theta_0}\hat{k})$$

comes from.

haruspex said:

The angles could be just an arbitrary example. Compare with the ensuing text where they use the location of MIT.

Let me back up one step. Where does the equation for ##\vec{\mu}## which seems to be ##\mu_E\hat{r(\theta_0,\phi_0})## come from? I thought the magnetic dipole moment of the Earth was a vector pointing along the rotation axis of the Earth?

In other words, if we are specifically doing the calculation for the Earth, how can the angles be just an arbitrary example?

The example uses ##\theta_0=169^{\circ}## and ##\phi_0=109^{\circ}##.

The meridian is thus ##109^{\circ}## west, and the latitude is ##90^{\circ}-169^{\circ}=-79^{\circ}##. This location is in Antarctica.

Therefore, this seems to be the accurate dipole moment vector of the Earth. I said in my previous post that the vector points along the rotation axis, but I knew that was only an approximation. I knew that the actual vector direction was off of the rotation axis by about 10 degrees and now I see that in fact the angles used by the cited notes bear this out.

So to answer my question about

$$\vec{\mu}_E=\mu_E(\sin{\theta_0}\cos{\phi_0}\hat{i}+\sin{\theta_0}\sin{\phi_0}\hat{j}+\cos{\theta_0}\hat{k})$$

this is literally just a position vector for the magnetic dipole moment. It is evaluated at the specific angles and magnitude which we know to be true from experiment.

zenterix said:

The example uses ##\theta_0=169^{\circ}## and ##\phi_0=109^{\circ}##.

The meridian is thus ##109^{\circ}## west, and the latitude is ##90^{\circ}-169^{\circ}=-79^{\circ}##. This location is in Antarctica.

Therefore, this seems to be the accurate dipole moment vector of the Earth. I said in my previous post that the vector points along the rotation axis, but I knew that was only an approximation. I knew that the actual vector direction was off of the rotation axis by about 10 degrees and now I see that in fact the angles used by the cited notes bear this out.

Ha! I considered the angle to the N magnetic pole, overlooking that the S magnetic pole is actually the N pole of the Earth's magnetic field.

zenterix said:

I have no idea where the equation
$$\vec{\mu}_E=\mu_E(\sin{\theta_0}\cos{\phi_0}\hat{i}+\sin{\theta_0}\sin{\phi_0}\hat{j}+\cos{\theta_0}\hat{k})$$
comes from.

A unit-vector ##\hat{n}##, satisfying ##\hat{n}\cdotp \hat{n}=1##, that in spherical coordinates ##\left(\theta,\phi\right)## points in the arbitrary direction ##\left(\theta_0,\phi_0\right)## is written in cartesian coordinates as: $$\hat{n}=\sin\theta_0\cos\phi_0\hat{i}+\sin\theta_0\sin\phi_0\hat{j}+\cos\theta_0\hat{k}$$Any vector ##\vec{v}## can be written as ##\vec{v}=\left\Vert \vec{v}\right\Vert \hat{n}##, so in particular the Earth's magnetic dipole-moment vector is:$$\vec{\mu}_{E}=\left\Vert \vec{\mu}_{E}\right\Vert \left(\cos\phi_{0}\sin\theta_{0}\hat{i}+\sin\phi_{0}\sin\theta_{0}\hat{j}+\cos\theta_{0}\hat{k}\right)$$

renormalize said:

A unit-vector ##\hat{n}##, satisfying ##\hat{n}\cdotp \hat{n}=1##, that in spherical coordinates ##\left(\theta,\phi\right)## points in the arbitrary direction ##\left(\theta_0,\phi_0\right)## is written in cartesian coordinates as: $$\hat{n}=\sin\theta_0\cos\phi_0\hat{i}+\sin\theta_0\sin\phi_0\hat{j}+\cos\theta_0\hat{k}$$Any vector ##\vec{v}## can be written as ##\vec{v}=\left\Vert \vec{v}\right\Vert \hat{n}##, so in particular the Earth's magnetic dipole-moment vector is:$$\vec{\mu}_{E}=\left\Vert \vec{\mu}_{E}\right\Vert \left(\cos\phi_{0}\sin\theta_{0}\hat{i}+\sin\phi_{0}\sin\theta_{0}\hat{j}+\cos\theta_{0}\hat{k}\right)$$

Yes, I am familiar with spherical coordinates. The issue is that initially I thought that equation the notes gave for ##\vec{\mu}_E## was a function of the angles when it is actually a fixed vector. I wasn't sure how the moment vector could be such a function. But now it makes sense. This particular part of the notes is simply giving us an example of real-world data for a dipole moment.