- #1
zenterix
- 423
- 60
- Homework Statement
- Below are links to an applet that allows one to tinker with sounds and their mathematical representation, and a document explaining how to use the applet.
- Relevant Equations
- My question will be about a specific snippet in the document that relates "higher harmonic" amplitude (which I think means a higher angular frequency pure tone with some amplitude) with fundamental frequency.
Here is an applet for playing around with Fourier coefficients and sounds.
Here is a document explaining a bit about the applet.
I did not quite understand everything.
Let me go through it.
Sound as perceived by humans is the physical phenomenon of variations in air pressure near the ear.
Audible sounds have variations starting at around ##0.2\cdot 10^4\text{Pa}## and go up to tens of thousands of ##\text{Pa}## of variation.
The size of the oscillations is related to the loudness of the sound.
The frequency of the oscillations is related to the pitch of the sound. Humans only perceive sounds within a certain frequency range.
Sound can be modeled by mathematical functions, in particular trigonometric functions.
A periodic function such as ##\sin{(2\pi\mathcal{v}t)}## represents a pure tone with frequency ##\mathcal{v}##.
The applet constructs a function
$$f(t)=\sum\limits_{n=0}^9 c_ne^{i(n\omega t+\phi)}\tag{1}$$
where the coefficients ##c_n## are complex.
There is a button that allows us to "toggle the restriction on the values of the coefficients making ##f(t)## real valued for ##n>0##" and when we select this option then "##c_{-n}## is reset to equal the complex conjugate of ##c_n##". This is because actually, (1) is
$$f(t)=\sum\limits_{n=-9}^9 c_ne^{i(n\omega t+\phi)}\tag{1b}$$
I'm not sure about what the negative subscript coefficients are at this point.
The document says the sound played corresponds to the function
$$\text{Re}(e^{i\phi}f(t))\tag{2}$$
But the help in the applet itself says the function is
$$\text{Re}(e^{-i\phi}f(t))\tag{3}$$
The applet allows us to change each of the first nine ##c_n## by selecting a magnitude and an argument.
We can also change ##\phi##.
We can also change the base frequency ##\mathcal{v}## (the selector is in ##kHz##. The resulting angular frequency is ##\omega = 2\pi\mathcal{v}\cdot 10^3##.
The aforementioned document contains the following snippet
I don't quite understand this.
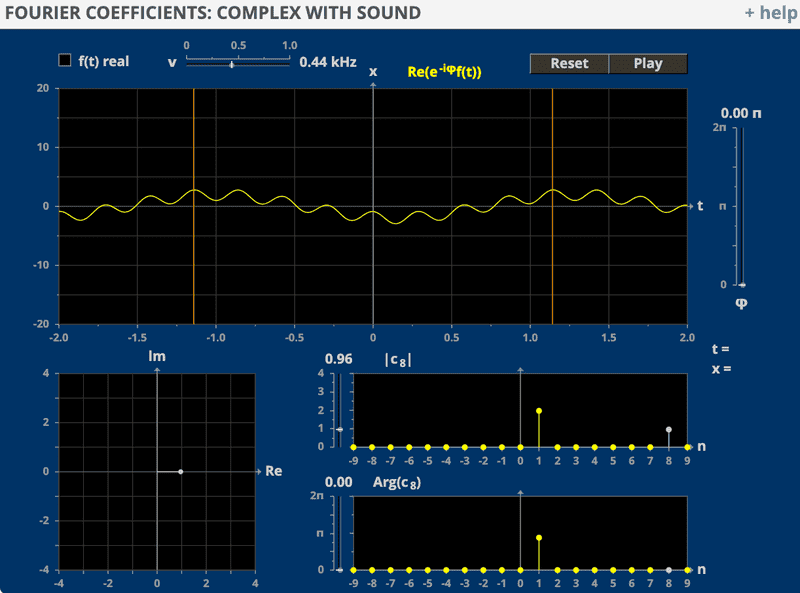
For example, suppose we choose ##\mathcal{v}=0.44\text{kHz}## and we are only taking the real part of (1) so that our sound becomes
$$2\cos{(440\pi t)}+\cos{(2\pi\cdot 440\cdot 8t)}$$
That is, we have a pure tone of 440Hz with coefficient ##c_1=2## and then we have coefficient ##c_8=1## which multiplies ##\cos{(16\cdot 440\pi t)}##.
If I understand correctly, both cosines have the same base frequency ##\mathcal{v}=440Hz##, but the cosine for ##c_8## has a much higher angular frequency. It is thus a "higher harmonic". The amplitude of the latter is ##c_8=1##.
How do we make it so that this higher harmonic has "much lower amplitude than the fundamental frequency"?
Here is the setup I have in the applet
Here is a document explaining a bit about the applet.
I did not quite understand everything.
Let me go through it.
Sound as perceived by humans is the physical phenomenon of variations in air pressure near the ear.
Audible sounds have variations starting at around ##0.2\cdot 10^4\text{Pa}## and go up to tens of thousands of ##\text{Pa}## of variation.
The size of the oscillations is related to the loudness of the sound.
The frequency of the oscillations is related to the pitch of the sound. Humans only perceive sounds within a certain frequency range.
Sound can be modeled by mathematical functions, in particular trigonometric functions.
A periodic function such as ##\sin{(2\pi\mathcal{v}t)}## represents a pure tone with frequency ##\mathcal{v}##.
The applet constructs a function
$$f(t)=\sum\limits_{n=0}^9 c_ne^{i(n\omega t+\phi)}\tag{1}$$
where the coefficients ##c_n## are complex.
There is a button that allows us to "toggle the restriction on the values of the coefficients making ##f(t)## real valued for ##n>0##" and when we select this option then "##c_{-n}## is reset to equal the complex conjugate of ##c_n##". This is because actually, (1) is
$$f(t)=\sum\limits_{n=-9}^9 c_ne^{i(n\omega t+\phi)}\tag{1b}$$
I'm not sure about what the negative subscript coefficients are at this point.
The document says the sound played corresponds to the function
$$\text{Re}(e^{i\phi}f(t))\tag{2}$$
But the help in the applet itself says the function is
$$\text{Re}(e^{-i\phi}f(t))\tag{3}$$
The applet allows us to change each of the first nine ##c_n## by selecting a magnitude and an argument.
We can also change ##\phi##.
We can also change the base frequency ##\mathcal{v}## (the selector is in ##kHz##. The resulting angular frequency is ##\omega = 2\pi\mathcal{v}\cdot 10^3##.
The aforementioned document contains the following snippet
If the higher harmonics have much lower amplitudes than the fundamental frequency, then the fundamental pitch will stay the same but the quality of the sound will change. If the amplitude of a higher harmonic approaches that of the fundamental you may begin to hear it as a separate note.
I don't quite understand this.
For example, suppose we choose ##\mathcal{v}=0.44\text{kHz}## and we are only taking the real part of (1) so that our sound becomes
$$2\cos{(440\pi t)}+\cos{(2\pi\cdot 440\cdot 8t)}$$
That is, we have a pure tone of 440Hz with coefficient ##c_1=2## and then we have coefficient ##c_8=1## which multiplies ##\cos{(16\cdot 440\pi t)}##.
If I understand correctly, both cosines have the same base frequency ##\mathcal{v}=440Hz##, but the cosine for ##c_8## has a much higher angular frequency. It is thus a "higher harmonic". The amplitude of the latter is ##c_8=1##.
How do we make it so that this higher harmonic has "much lower amplitude than the fundamental frequency"?
Here is the setup I have in the applet
Last edited: