- #1
chwala
Gold Member
- 2,573
- 343
- Homework Statement
- See attached
- Relevant Equations
- cubic equations and roots.
The problem and solution are posted... no. 8
I may need insight on common difference ...

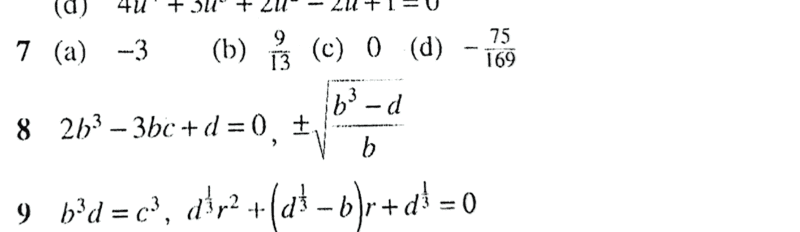
In my lines i have,
Let the roots be ##(b), (b-1)## and ##(b+1)##.
Then,
##x^3-3bx^2+3cx-d = a(x-b(x-b+1)(x-b-1)##
##x^3-3bx^2+3cx-d= a(x^3-3bx^2+3b^2x-x-b^3+b)##
##a=1##.
Let
##f(x)=x^3-3bx^2+3b^2x-x-b^3+b##
Using Factor theorem,
##f(b)=b^3-3b^3+3b^3-b-b^3+b=0##
##f(b)=0## thus ##b## is a root of the cubic equation.
For the condition, we solve the equations,
##x^3-3bx^2+3cx-d= x^3-3bx^2+3b^2x-x-b^3+b##
##(3b^2-1)=3c##
##-b^3+b=-d##
##⇒b(b^2-(3b^2-3c))=d##
##b(-2b^2+3c)=d##
##2b^3-3bc+d=0##.
Any insight ...let me work on common difference later...
I may need insight on common difference ...
In my lines i have,
Let the roots be ##(b), (b-1)## and ##(b+1)##.
Then,
##x^3-3bx^2+3cx-d = a(x-b(x-b+1)(x-b-1)##
##x^3-3bx^2+3cx-d= a(x^3-3bx^2+3b^2x-x-b^3+b)##
##a=1##.
Let
##f(x)=x^3-3bx^2+3b^2x-x-b^3+b##
Using Factor theorem,
##f(b)=b^3-3b^3+3b^3-b-b^3+b=0##
##f(b)=0## thus ##b## is a root of the cubic equation.
For the condition, we solve the equations,
##x^3-3bx^2+3cx-d= x^3-3bx^2+3b^2x-x-b^3+b##
##(3b^2-1)=3c##
##-b^3+b=-d##
##⇒b(b^2-(3b^2-3c))=d##
##b(-2b^2+3c)=d##
##2b^3-3bc+d=0##.
Any insight ...let me work on common difference later...