- #1
Weightlifting
- 10
- 2
- Homework Statement
- Find the vertical asymptote of ##y=\frac{2x-5}{\left|3x+2\right|}##. If there is an infinite limit, what direction does it go in?
- Relevant Equations
- Note: I'm currently only at the stage of using the informal definition of limits ("Calculus, a complete course" by Robert A. Adams, chapter 1.3, 9th edition, problem 34, to be exact), so I'm looking for help without using the epsilon-delta method
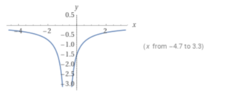
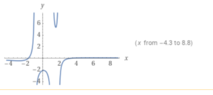
Since ##\left|3x+2\right|=0\rightarrow\ x=-\frac{2}{3}##, we know the vertical asymptote is at ##x=-\frac{2}{3}##.
Looking at the limit at that point, and also looking at the left- and right-sided limit, I cannot simplify it any further: ##\lim_{x\rightarrow-\frac{2}{3}}{\frac{2x-5}{\left|3x+2\right|}}=\lim_{x\rightarrow-\frac{2}{3}\pm}{\frac{2x-5}{\pm(3x+2)}}##.
That being said, is there an easy way to find out whether the limit is going towards infinity, and which direction the infinity goes? Or should I be expected to be able to quickly visualize what a graph of a function looks like, and determine from there which direction the graph goes? Right now, I just plotted it using computer software to see that the direction of the limit goes towards negative infinity, see attachment. However, Is there a method to quickly determine this without using software?
Thank you!
Looking at the limit at that point, and also looking at the left- and right-sided limit, I cannot simplify it any further: ##\lim_{x\rightarrow-\frac{2}{3}}{\frac{2x-5}{\left|3x+2\right|}}=\lim_{x\rightarrow-\frac{2}{3}\pm}{\frac{2x-5}{\pm(3x+2)}}##.
That being said, is there an easy way to find out whether the limit is going towards infinity, and which direction the infinity goes? Or should I be expected to be able to quickly visualize what a graph of a function looks like, and determine from there which direction the graph goes? Right now, I just plotted it using computer software to see that the direction of the limit goes towards negative infinity, see attachment. However, Is there a method to quickly determine this without using software?
Thank you!
Attachments
Last edited: