- #1
songoku
- 2,266
- 319
- Homework Statement
- Please see below
- Relevant Equations
- P(X = a) = ##\int_{a}^{a} f(x) dx = 0##
Derivative of CDF = PDF
This is part of my note:
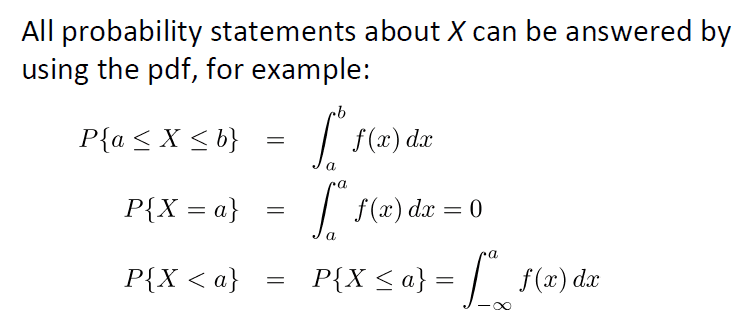
Now, this is practice question:

I want to ask why P(X = 2) is not zero, because from the note: P{X = a} = ##\int_{a}^{a} f(x) dx=0## ?
If I differentiate F(x), I will get f(x) which is the pdf, then using the pdf to find P(X = 2), I think I will get zero as the probability.
Thanks
Now, this is practice question:
I want to ask why P(X = 2) is not zero, because from the note: P{X = a} = ##\int_{a}^{a} f(x) dx=0## ?
If I differentiate F(x), I will get f(x) which is the pdf, then using the pdf to find P(X = 2), I think I will get zero as the probability.
Thanks