- #1
Steels
- 3
- 0
- Homework Statement
- Galileo Ratio? But why squeroot? what am i missing?
- Relevant Equations
- s=u*t+a*t^2/2 VS 1:2:3:... t1/t10=s1/s10?
Hello! I can do this task just using this formula s=u*t+a*t^2/2.
But just saw an example where someone used this Galileo toerem.
Here is task:
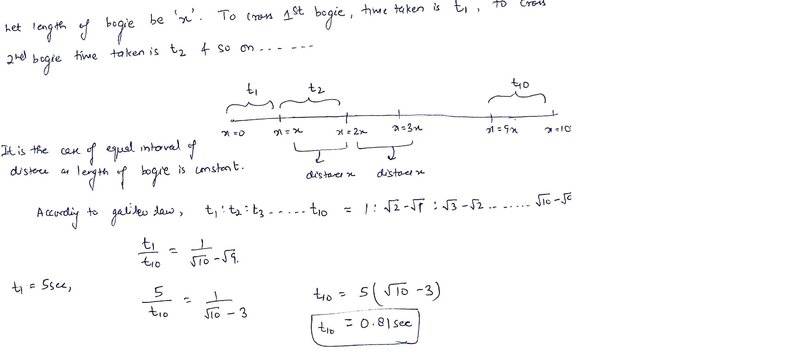
"An observer stands on the platform at the front edge of the first bogie of a stationary train. The train starts moving with uniform acceleration and the first bogie takes 5 seconds to cross the observer. If all the bogies of the train are of equal length and the gap between them is negligible, the time taken by the tength bogie to cross observer is?"
Now please, if you look at picture, you see its t1/t10=1/(sqrt(10)-sqrt(9))My question is, why its in squeroot? Where do we get x^2? so to get squeroot we need x^2! but from what? Why the lenght, it its meter it should be as meter, so where we get m^2? What am i doing wrong. Thanks for any explenation!
But just saw an example where someone used this Galileo toerem.
Here is task:
"An observer stands on the platform at the front edge of the first bogie of a stationary train. The train starts moving with uniform acceleration and the first bogie takes 5 seconds to cross the observer. If all the bogies of the train are of equal length and the gap between them is negligible, the time taken by the tength bogie to cross observer is?"
Now please, if you look at picture, you see its t1/t10=1/(sqrt(10)-sqrt(9))My question is, why its in squeroot? Where do we get x^2? so to get squeroot we need x^2! but from what? Why the lenght, it its meter it should be as meter, so where we get m^2? What am i doing wrong. Thanks for any explenation!
 ##\qquad ## !
##\qquad ## !
