- #1
runinfang
- 3
- 0
- Homework Statement
- Verify Stokes' theorem in the plane where f(x,y)=y2i+x2j
and the region formed is bounded by the circle (x^2+y^2=4).
- Relevant Equations
- Stokes' theorem in the plane
"Let \( M \) and \( N \) be the functions, \( C \) be the curve, and \( R \) be the region defined as in Green's theorem. If \( \mathbf{F}(x, y) = M(x, y)\mathbf{i} + N(x, y)\mathbf{j} \) and \( \mathbf{T}(s) \) is the unit tangent vector to \( C \) at \( P \), where \( s \) units is the arc length of \( C \) measured from a point \( P_0 \) to \( P \), then:
\[
\oint_C \mathbf{F} \cdot \mathbf{T} \, ds = \iint_R (\text{curl } \mathbf{F}) \cdot \mathbf{k} \, dA
\]"
The question is a problem from Leithold's calculus book. I didn't understand the (x = 5 \cos(t)). Shouldn't it be (x = 2 cos(t))? I'm referring to item b.

i tried this way. i don't know what is wrong.
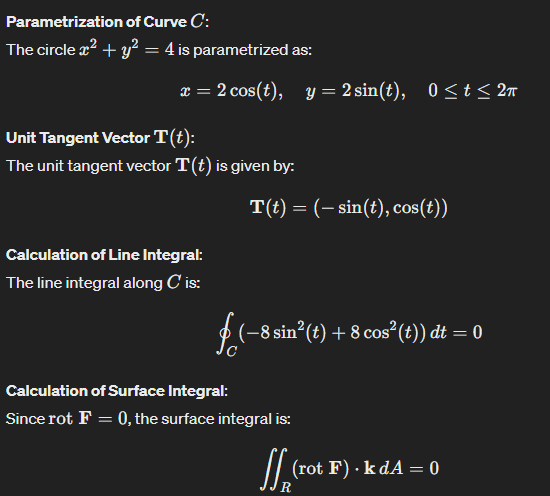
i tried this way. i don't know what is wrong.
Last edited: