- #1
zenterix
- 423
- 60
- Homework Statement
- I've been learning about Fourier series and I have a few questions.
- Relevant Equations
- Consider the function
$$f(t)=\begin{cases} 2\ \ \ \ \ 0<t<\pi/2 \\ 0\ \ \ \ \ \frac{\pi}{2}<t<\pi\end{cases}$$
Here is a plot
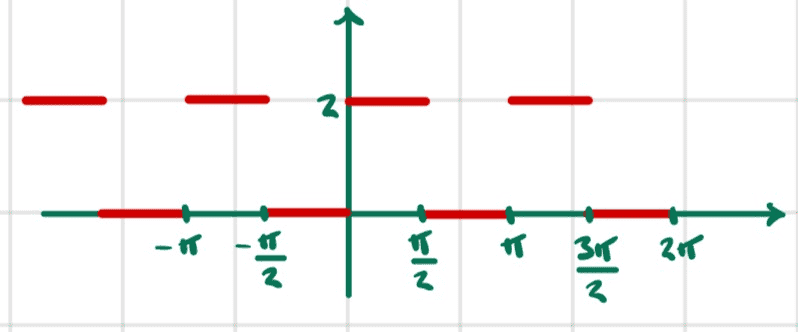
We see that this function has minimal period of ##\pi##.
Initially, the material was presented with functions that had a period of ##2\pi## and were explicitly defined on the interval ##[-\pi,\pi]## and defined everywhere else by ##f(x+n2\pi)=f(x)##.
Then it was shown that actually, if the period is ##2L## we can rescale ##[-\pi,\pi]## to ##[-L,L]## and we get essentially the same formulas for the Fourier coefficients.
I want to make sure of the following
The function ##f## was defined above in terms of an interval ##[0,\pi]##.
We could obtain formulas for the coefficients in terms of integrals of this interval. The only difference is that the formulas would be substantially more complicated since we would no longer be making use of the same simple orthogonality conditions of the ##\sin## and ##\cos## functions used to derive the coefficients when we are using an interval symmetric about the origin?
Another thing I want to be sure of is the following
We define a periodic function. Then we define a Fourier series which is made up of continuous trigonometric functions defined on the entire real line.
The problem of defining under what conditions the Fourier series equals the function is solved for a large class of functions by Dirichlet's theorem, which basically says that if
1) ##f(x)## is defined and bounded for ##\pi\leq x<\pi## with only a finite number of discontinuities and finite number of maxima and minima on this interval and
2) ##f(x)## is defined for ##x## outside this interval by ##f(x+2\pi)=f(x)##
Then, for any point ##x## the Fourier series converges to the average of the right and left-hand limits of ##f## at this point.
This means that the Fourier series is equal to ##f## at every continuous point.
For the Fourier series to equal ##f## at the points of discontinuity, ##f## would have to be defined at those points to the the average of right and left-hand limits of ##f## at that point.
My third question is if the following is true.
The important things are that ##f## be periodic (which is essentially condition 2 above) and that on an interval representing one period, condition 1) be true.
This means that considering ##f## in the example given at the start of this post, if we shift it in time such that it is no longer symmetric about the ##y##-axis this does not change the fact that we can compute the Fourier coefficients.
##g(t)=f(t+\frac{\pi}{4})## is not symmetric about the ##y##-axis. The formulas for the coefficients of the Fourier series of ##g## would be more complicated. However, for such functions (which are the result of shifting and scaling of functions that are symmetric about the ##y##-axis) we use mathematical tricks to find the coefficients rather than computing them directly. In the case of ##g##, we simply take the Fourier series of ##f## and substitute ##t+\pi/4## for ##t##.
We see that this function has minimal period of ##\pi##.
Initially, the material was presented with functions that had a period of ##2\pi## and were explicitly defined on the interval ##[-\pi,\pi]## and defined everywhere else by ##f(x+n2\pi)=f(x)##.
Then it was shown that actually, if the period is ##2L## we can rescale ##[-\pi,\pi]## to ##[-L,L]## and we get essentially the same formulas for the Fourier coefficients.
I want to make sure of the following
The function ##f## was defined above in terms of an interval ##[0,\pi]##.
We could obtain formulas for the coefficients in terms of integrals of this interval. The only difference is that the formulas would be substantially more complicated since we would no longer be making use of the same simple orthogonality conditions of the ##\sin## and ##\cos## functions used to derive the coefficients when we are using an interval symmetric about the origin?
Another thing I want to be sure of is the following
We define a periodic function. Then we define a Fourier series which is made up of continuous trigonometric functions defined on the entire real line.
The problem of defining under what conditions the Fourier series equals the function is solved for a large class of functions by Dirichlet's theorem, which basically says that if
1) ##f(x)## is defined and bounded for ##\pi\leq x<\pi## with only a finite number of discontinuities and finite number of maxima and minima on this interval and
2) ##f(x)## is defined for ##x## outside this interval by ##f(x+2\pi)=f(x)##
Then, for any point ##x## the Fourier series converges to the average of the right and left-hand limits of ##f## at this point.
This means that the Fourier series is equal to ##f## at every continuous point.
For the Fourier series to equal ##f## at the points of discontinuity, ##f## would have to be defined at those points to the the average of right and left-hand limits of ##f## at that point.
My third question is if the following is true.
The important things are that ##f## be periodic (which is essentially condition 2 above) and that on an interval representing one period, condition 1) be true.
This means that considering ##f## in the example given at the start of this post, if we shift it in time such that it is no longer symmetric about the ##y##-axis this does not change the fact that we can compute the Fourier coefficients.
##g(t)=f(t+\frac{\pi}{4})## is not symmetric about the ##y##-axis. The formulas for the coefficients of the Fourier series of ##g## would be more complicated. However, for such functions (which are the result of shifting and scaling of functions that are symmetric about the ##y##-axis) we use mathematical tricks to find the coefficients rather than computing them directly. In the case of ##g##, we simply take the Fourier series of ##f## and substitute ##t+\pi/4## for ##t##.