- #1
docnet
Gold Member
- 672
- 307
- Homework Statement
- .
- Relevant Equations
- .
The below image is an excerpt from a website about Markov Chains.
In the red boxed which I put in the image, I don't understand why the term ##g(i)## isn't being summed over ##j## instead of ##i##, since the outer sum is over the ##i##th element of the vector ##Pg##, which is the dot product between the ##i##th row of ##P## and ##g##.
I expected ##\langle f,Pg \rangle## to expand as $$\sum_i f(i)(Pg)_i \pi_i = \sum_i f(i)\Big(\sum_jP_{ij}g(j)\Big)\pi_i .$$
But, the website shows $$\langle f,Pg \rangle= \sum_i f(i)\Big(\sum_jP_{ij}g(i)\Big)\pi_i .$$ What am I misunderstanding?

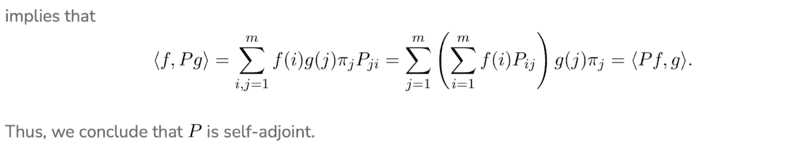
In the red boxed which I put in the image, I don't understand why the term ##g(i)## isn't being summed over ##j## instead of ##i##, since the outer sum is over the ##i##th element of the vector ##Pg##, which is the dot product between the ##i##th row of ##P## and ##g##.
I expected ##\langle f,Pg \rangle## to expand as $$\sum_i f(i)(Pg)_i \pi_i = \sum_i f(i)\Big(\sum_jP_{ij}g(j)\Big)\pi_i .$$
But, the website shows $$\langle f,Pg \rangle= \sum_i f(i)\Big(\sum_jP_{ij}g(i)\Big)\pi_i .$$ What am I misunderstanding?


