A Novel Technique of Calculating Unit Hypercube Integrals

Introduction

In this insight article, we will build all the machinery necessary to evaluate unit hypercube integrals by a novel technique. We will first state a theorem on Dirichlet integrals, second develop a sequence of nested sets that point-wise converges to a unit hypercube, and thirdly make these two pieces compatible by means of a Dominated Convergence Theorem, and lastly demonstrate the technique of integration. Note: The same technique is outlined (in the same way) in the expanded insight article entitled A Path to Fractional Integral Representations of Some Special Functions.

The Integrals of Dirichlet

Dirichlet integrals as I learned them from an Advanced Calculus book are just that formula evaluating the integral to Gamma functions, they are not a type of integral like Riemann integral, more just a formula that would go on a table of integrals. Content is the 4+-dimensional version of volume (some writers use hypervolume instead of content).

For the proof of this Dirichlet Integrals Theorem, I refer the reader to the text Special Functions by Askey, Andrews, and Roy. The result due to Dirichlet is given by

Theorem 1.1: Dirichlet Integrals

If ##t,{\alpha _p},{\beta _q},\Re \left[ {{\gamma _r}} \right] > 0\forall p,q,r## and ##V_t^n: = \left\{ {\left( {{z_1},{z_2}, \ldots ,{z_n}} \right) \in {\mathbb{R}^n}|{z_j} \geq 0\forall j,\sum\limits_{k = 1}^n {{{\left( {\frac{{{z_k}}}{{{\alpha _k}}}} \right)}^{{\beta _k}}} \leq t} } \right\}##, then

$$\iint {\mathop  \cdots \limits_{V_t^n} \int {\prod\limits_{\lambda  = 1}^n {\left( {z_\lambda ^{{\gamma _\lambda } – 1}} \right)} d{z_n} \ldots d{z_2}d{z_1}} } = {t^{\sum\limits_{p = 1}^n {\frac{{{\gamma _p}}}{{{\beta _p}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\frac{{\alpha _q^{{\gamma _q}}}}{{{\beta _q}}}\Gamma \left( {\frac{{{\gamma _q}}}{{{\beta _q}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\frac{{\alpha _q^{{\gamma _q}}}}{{{\beta _q}}}\Gamma \left( {\frac{{{\gamma _q}}}{{{\beta _q}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\frac{{{\gamma _k}}}{{{\beta _k}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\frac{{{\gamma _k}}}{{{\beta _k}}}} } \right)}}$$

Corollary 1.2: Content Integral

If ##{\alpha _p},{\beta _q} > 0\forall p,q## and ##{V^n}: = \left\{ {\left( {{z_1},{z_2}, \ldots ,{z_n}} \right) \in {\mathbb{R}^n}|{z_j} \geq 0\forall j,\sum\limits_{k = 1}^n {{{\left( {\frac{{{z_k}}}{{{\alpha _k}}}} \right)}^{{\beta _k}}} \leq 1} } \right\}##, then

##{\text{Content}}\left( {{V^n}} \right): = \iint {\mathop  \cdots \limits_{{V^n}} \int {d{z_n} \ldots d{z_2}d{z_1}} } = {{\prod\limits_{q = 1}^n {\left[ {\frac{{{\alpha _p}}}{{{\beta _q}}}\Gamma \left( {\frac{1}{{{\beta _q}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\frac{{{\alpha _p}}}{{{\beta _q}}}\Gamma \left( {\frac{1}{{{\beta _q}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\frac{1}{{{\beta _k}}}} } \right)}}} \right.} {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\frac{1}{{{\beta _k}}}} } \right)}}##. Where content refers to hypervolume when ##n \geq 4##.

The Orthotope

The orthotope is the generalization of the rectangular parallelepiped to ##{\mathbb{R}^n}##. Let ##{b_k} > 0\forall k \leq n## and consider the orthotope with polytope vertices of the form ##\left( { \pm {b_1}, \pm {b_2}, \ldots , \pm {b_n}} \right)## orientated with facet-centered axes determined by the set ##{P^n}: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\left| {{x_k}} \right| \leq {b_k}\forall k \leq n} \right\}##. It will be convenient to develop a definition of the orthotope which may seem overly complicated but will make good use of it in the next section. Let ##S_N^n: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N}}}  \leq n} \right\}##. Then we proceed to prove by bivariate induction on n and N that

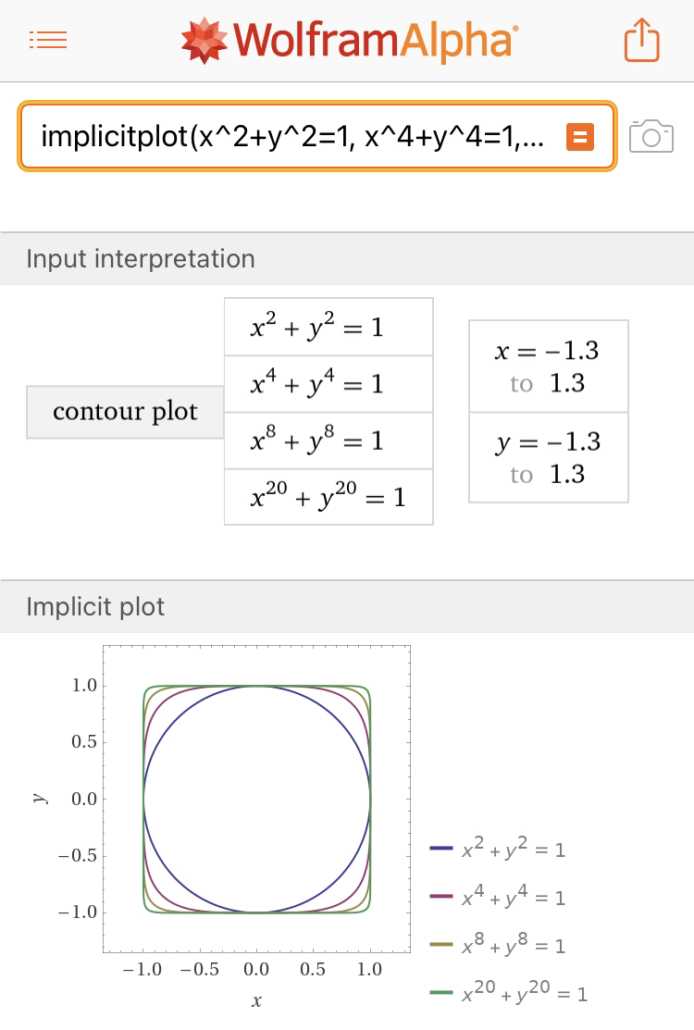
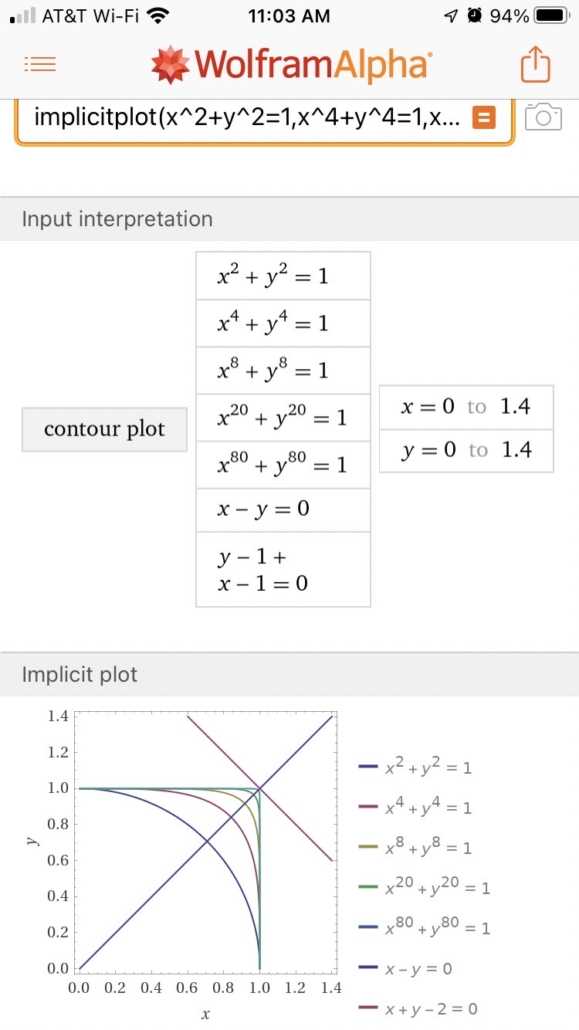
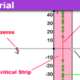
Images of the 2-d versions of the some of the sequence of sets ##S_N^2## and the geometry of the next heading’s method of finding extrema

Lemma 2.1: Nesting Property of ##S_N^n##

If ##S_N^n: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N}}}  \leq n} \right\}##, then ##S_{N + 1}^n \subset S_N^n##.

Proof:

By bivariate induction on n and N (this has three parts)[1]:

First, we define the statement to be proved ##P\left( {n,N} \right):S_{N + 1}^n \subset S_N^n##.

(i) Prove the base case ##P\left( {a,b} \right)## where ##a,b \in {\mathbb{Z}^ + }## are the base or smallest values of a and b such that ##P\left( {a,b} \right)## holds. For this problem that means proving ##P\left( {2,1} \right):S_2^2 \subset S_1^2##. We have ##S_2^2: = \left\{ {\left( {{x_1},{x_2}} \right) \in {\mathbb{R}^2}|\sum\limits_{k = 1}^2 {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^4}}  \leq 2} \right\}## implies the following inequality holds ##\sum\limits_{k = 1}^2 {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^4}}  \leq 2##. Now to work given inequality down we will use calculus to find the values that maximize the constraint ##f\left( {{x_1},{x_2}} \right) = \sum\limits_{k = 1}^2 {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^4}}  \leq 2## and the ad hoc constraint ##g\left( {{x_1},{x_2}} \right) = \tfrac{{{x_1}}}{{{b_1}}} + \tfrac{{{x_2}}}{{{b_2}}} = c## for some positive constant c (which is certainly true). We proceed by the method of Lagrange multipliers

Example 2-d S_N^2 sets for extrema

$$\nabla f = \left\langle {4\tfrac{{x_1^3}}{{b_1^4}},4\tfrac{{x_2^3}}{{b_2^4}}} \right\rangle  = \lambda \left\langle {\tfrac{1}{{{b_1}}},\tfrac{1}{{{b_2}}}} \right\rangle  = \lambda \nabla g \Rightarrow \lambda  = 4{\left( {\tfrac{{{x_1}}}{{{b_1}}}} \right)^3} = 4{\left( {\tfrac{{{x_2}}}{{{b_2}}}} \right)^3} \Leftrightarrow {x_2} = \tfrac{{{b_2}}}{{{b_1}}}{x_1}$$

Plug this relation into the former inequality, namely

##f\left( {{x_1},\tfrac{{{b_2}}}{{{b_1}}}{x_1}} \right) = {\left( {\tfrac{{{x_1}}}{{{b_1}}}} \right)^4} + {\left( {\tfrac{{{x_1}}}{{{b_1}}}} \right)^4} \leq 2 \Rightarrow {\left( {\tfrac{{{x_1}}}{{{b_1}}}} \right)^2} \leq 1 = :{\max _{1 \leq i \leq 2}}\left\{ {{{\left( {\frac{{{x_i}}}{{{b_i}}}} \right)}^2}} \right\}##

where ##{\max _{1 \leq i \leq n}}\left\{ {{a_i}} \right\}: = \max \left\{ {{a_1},{a_2}, \ldots ,{a_n}} \right\}##. Checking to see if ##S_2^2 \subset S_1^2## by plugging in maximal values we get ##\sum\limits_{k = 1}^2 {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^2}}  \leq 2{\max _{1 \leq i \leq 2}}\left\{ {{{\left( {\frac{{{x_i}}}{{{b_i}}}} \right)}^2}} \right\} = 2##, and hence ##S_2^2 \subset S_1^2## the base case is proven to hold.

(ii) Now we prove induction over n: assume that ##P\left( {n,b} \right)## holds for some fixed ##n \in {\mathbb{Z}^ + }## and where b is as in part (i). Then we need to prove that ##P\left( {n + 1,b} \right)## is therefore true. For this problem that means proving ##P\left( {n,1} \right):S_2^n \subset S_2^n \Rightarrow P\left( {n + 1,1} \right):S_2^{n + 1} \subset S_2^{n + 1}##.

Assume $$P\left( {n,1} \right) :S_2^n: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^4}}  \leq n} \right\} \subset \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}| \sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^2}}  \leq n} \right\} = :S_1^n$$ (it turns out we will not need this assumption to prove what needs to be proven, just some simple calculus). Now let’s look at

$$P\left( {n + 1,1} \right):S_2^{n + 1}: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_{n + 1}}} \right) \in {\mathbb{R}^{n + 1}}|\sum\limits_{k = 1}^{n + 1} {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^4}}  \leq n + 1} \right\} \subset \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_{n + 1}}} \right) \in {\mathbb{R}^{n + 1}}|\sum\limits_{k = 1}^{n + 1} {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^2}}  \leq n + 1} \right\} = :S_1^{n + 1}$$

Let us just use calculus to maximize the function ##F\left( {\vec x} \right): = \sum\limits_{k = 1}^{n + 1} {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^2}} ## subject to the constraint  ##G\left( {\vec x} \right): = \sum\limits_{k = 1}^{n + 1} {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^4}}  \leq n + 1 ##. Using the method of Lagrange Multipliers again we have (in component form): $${\left( {\nabla F} \right)_i} = 2\tfrac{{{x_i}}}{{b_i^2}} = 4\lambda \tfrac{{x_i^3}}{{b_i^4}} = \lambda {\left( {\nabla G} \right)_i} \Rightarrow \left( {{x_i} = 0} \right) \vee \left[ {\left( {{x_i} \ne 0} \right) \wedge \left( {\lambda  = \tfrac{1}{2}{{\left( {\tfrac{{{b_i}}}{{{x_i}}}} \right)}^2}} \right)} \right] $$ $$\Rightarrow {z^2}: = {\left( {\tfrac{{{x_i}}}{{{b_i}}}} \right)^2} = {\left( {\tfrac{{{x_j}}}{{{b_j}}}} \right)^2}\,\forall i \ne j \leq n + 1$$ is when the maximum occurs because obviously the zero was a minimum. Plugging into the constraint to get a bound for ##{z^2}## gives ##\sum\limits_{k = 1}^{n + 1} {{z^4}}  = \left( {n + 1} \right){z^4} \leq n + 1 \Rightarrow {z^2} \leq 1## and then to find the actual maximum we get ##F\left( {\vec x} \right) \leq \sum\limits_{k = 1}^{n + 1} {{z^2}}  = \left( {n + 1} \right){z^2} = n + 1## and hence ##S_2^{n + 1} \subset S_1^{n + 1}##.

(iii) Now for the induction on N step: Assume ##P\left( {n,N} \right)##  holds for some fixed N. We must prove that ##P\left( {n,N + 1} \right)## is therefore true. Notably we will not use the assumption in this step. We have ##S_{N + 2}^n: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N + 4}}}  \leq n} \right\}##. From this the inequality ##\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N + 4}}}  \leq n## holds for fixed N, so we should maximize ##\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N + 2}}}##  subject to that constraint: proceeding by Lagrange Multipliers method in component form we have ##\left( {2N + 2} \right)\tfrac{{x_k^{2N + 1}}}{{b_k^{2N + 2}}} = \left( {2N + 4} \right)\lambda \tfrac{{x_k^{2N + 3}}}{{b_k^{2N}}} \Rightarrow \frac{{N + 1}}{{N + 2}}\tfrac{{b_k^2}}{{x_k^2}} = \lambda  \Rightarrow w: = \tfrac{{x_k^2}}{{b_k^2}} = \tfrac{{x_j^2}}{{b_j^2}}\forall j \ne k \leq n## now plug this value into the constraint to get ##\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N + 4}}}  = \sum\limits_{k = 1}^n {{w^{2N + 4}}}  = n{w^{2N + 4}} \leq n \Rightarrow w = 1## which value we plug into the function being maximized to determine the maximum to be ##\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N + 2}}}  \leq \sum\limits_{k = 1}^n {{w^{2N + 2}}}  = n## thus ##S_{N + 2}^n \subset S_{N + 1}^n##. Hence the lemma is true.

Theorem 2.2: Equivalence of ##S^n## to ##P^n##

If ##S_N^n: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N}}}  \leq n} \right\}## and if ##{P^n}: = \left\{ {\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) \in {\mathbb{R}^n}|\left| {{x_k}} \right| \leq {b_k}\forall k \leq n} \right\}##. Then ##{S^n} \subset  \cdots  \subset S_{N + 1}^n \subset S_N^n \subset  \cdots  \subset S_1^n## where ##{S^n}: = \bigcap\limits_{j = 1}^\infty  {S_j^n} ## and ##{S^n} = {P^n}##.

Proof:

That ##{S^n} \subset  \cdots  \subset S_{N + 1}^n \subset S_N^n \subset  \cdots  \subset S_1^n## we have lemma 2.1 and that if ##\vec x \in {S^n}: = \bigcap\limits_{j = 1}^\infty  {S_j^n} ##, then ##\vec x \in S_N^n\forall N \in {\mathbb{Z}^ + }##. For the equality ##{S^n} = {P^n}##, suppose ##\exists \vec y \in S\left( {{S^n},{P^n}} \right) = \left( {{S^n} – {P^n}} \right) \cup \left( {{P^n} – {S^n}} \right)## , where ##S\left( {A,B} \right)## is the symmetric difference of sets A and B. Then either

(i) $$\begin{gathered}\exists \vec y \in \left( {{S^n} – {P^n}} \right) = \left\{ {\vec x \in {\mathbb{R}^n}|\left( {\vec x \in {S^n}} \right) \wedge \left( {\vec x \notin {P^n}} \right)} \right\} \\ = \left\{ {\vec x \in {\mathbb{R}^n}|\vec x \in {S^n} = \mathop {\lim }\limits_{M \to \infty } \,\bigcap\limits_{j = 1}^M {S_j^n}  = \mathop {\lim }\limits_{M \to \infty } S_M^n\,} \right\} \cap \left\{ {\vec x \in {\mathbb{R}^n}|\exists k \in {\mathbb{Z}^ + } \mathrel\backepsilon  \left( {1 \leq k \leq n} \right) \wedge \left( {\tfrac{{\left| {{x_k}} \right|}}{{{b_k}}} > 1} \right)} \right\} \\ \end{gathered}$$

where we have applied $${S^n} \subset  \cdots  \subset S_{N + 1}^n \subset S_N^n \subset  \cdots  \subset S_1^n$$ in the evaluation of the limit. Furthermore $$\exists k \in {\mathbb{Z}^ + } \mathrel\backepsilon  \left( {1 \leq k \leq n} \right) \wedge \left( {\tfrac{{\left| {{x_k}} \right|}}{{{b_k}}} > 1} \right) \Rightarrow \exists \varepsilon  > 0 \mathrel\backepsilon  \tfrac{{\left| {{x_k}} \right|}}{{{b_k}}} = 1 + \varepsilon  \Rightarrow \exists M \in {\mathbb{Z}^ + } \mathrel\backepsilon  N \geq M \Rightarrow \sum\limits_{j = 1}^n {{{\left( {\frac{{{x_j}}}{{{b_j}}}} \right)}^{2N}}}  > n$$

Even for the minimal condition that ##{x_j} = 0\forall j \ne k \leq n## we have by the binomial theorem that $$\sum\limits_{j = 1}^n {{{\left( {\frac{{{x_j}}}{{{b_j}}}} \right)}^{2N}}}  = {\left( {1 + \varepsilon } \right)^{2N}} = \sum\limits_{j = 1}^{2N} {\left( {\left. {\begin{array}{*{20}{c}}{2N} \\ j \end{array}} \right)} \right.} \,{\varepsilon ^j} = 1 + 2N\varepsilon  + N\left( {2N – 1} \right){\varepsilon ^2} +  \cdots$$  so choose ##N \in {\mathbb{Z}^ + } \mathrel\backepsilon  2N\varepsilon  \geq n \Rightarrow N = \left\lceil {\tfrac{{n – 1}}{{2\varepsilon }}} \right\rceil##   and hence ##\left( {{S^n} – {P^n}} \right) = \emptyset##  a contradiction.

Or (ii)

$$\begin{gathered}\exists \vec y \in \left( {{P^n} – {S^n}} \right) = \left\{ {\vec x \in {\mathbb{R}^n}|\left( {\vec x \in {P^n}} \right) \wedge \left( {\vec x \notin {S^n}} \right)} \right\} \\ = \left\{ {\vec x \in {\mathbb{R}^n}|\tfrac{{\left| {{x_k}} \right|}}{{{b_k}}} \leq 1{\text{ for }}k = 1,2, \ldots ,n\,} \right\} \cap \left\{ {\vec x \in {\mathbb{R}^n}|\vec x \notin \bigcap\limits_{j = 1}^\infty  {S_j^n} } \right\} \\ \end{gathered}$$

we have from the left-hand set ##\tfrac{{\left| {{x_k}} \right|}}{{{b_k}}} \leq 1## for ##k = 1,2, \ldots ,n##, which implies that $$\forall N \in {\mathbb{Z}^ + },\sum\limits_{j = 1}^n {{{\left( {\frac{{{x_j}}}{{{b_j}}}} \right)}^{2N}}}  \leq n \cdot {1^{2N}} = n \Rightarrow \vec x \in \bigcap\limits_{j = 1}^\infty  {S_j^n}$$ so that ##\left( {{P^n} – {S^n}} \right) = \emptyset ##, a contradiction. Having found contradictions in both cases (i) and (ii) we conclude $$S\left( {{S^n},{P^n}} \right) = \left( {{S^n} – {P^n}} \right) \cup \left( {{P^n} – {S^n}} \right) = \emptyset $$ a contradiction to the former assumption proving ##{S^n} = {P^n}##.

Unit Hypercube Integrals

For reference, we state here the Lebesgue Dominated Convergence Theorem,

Theorem 3.1 (DCT): Lebesgue Dominated Convergence Theorem

Suppose ##E \in \mathfrak{M}## (the family of measurable sets). Let ##\left\{ {{f_n}} \right\}##  be a sequence of measurable functions such that ##{f_n}\left( x \right) \to f\left( x \right)## almost everywhere on E as ##n \to \infty ##. If there exists a function ##g \in \mathfrak{L}\left( \mu  \right)## on E (g is Lebesgue integrable with respect to ##\mu ## on E), such that ##\left| {{f_n}\left( x \right)\,} \right| \leq g\left( x \right)##, for ##n = 1,2,3, \ldots## and ##\forall x \in E##, then $$\mathop {\lim }\limits_{n \to \infty } \,\int_E {{f_n}d\mu }  = \int_E {fd\mu } $$[2]

Theorem 3.2: Dominated Convergence Theorem with Nesting Property

Let ##{A_n},A \subset {\mathbb{R}^n}## and ##{A_n},A \in \mathfrak{M}## for ##n \in {\mathbb{Z}^ + }## such that $$A \subset  \cdots  \subset {A_{n + 1}} \subset {A_n} \subset  \cdots  \subset {A_1}$$ and let ##A: = \bigcap\limits_{j = 1}^\infty  {{A_j}} ##. Then for Lebesgue measurable ##f:{\mathbb{R}^n} \to \mathbb{C}## define the set function ##\phi :{A_1} \to \mathbb{C}## by

$$\phi \left( E \right): = \int_E {fd\mu } ,\forall E \subset {A_1}$$ Then $$\mathop {\lim }\limits_{n \to \infty } \,\phi \left( {{A_n}} \right) = \phi \left( A \right)$$ which is to say explicitly that $$\mathop {\lim }\limits_{n \to \infty } \,\int_{{A_n}} {fd\mu }  = \int_A {fd\mu }$$

Proof:

Define ##{\chi _E}\left( x \right): = \left\{ {\begin{array}{*{20}{c}}{1,}&{x \in E} \\ {0,}&{x \notin E}\end{array}} \right.##

the characteristic function of the set E. Then let ##{f_n}: = f \circ {\chi _{\bigcap\limits_{j = 1}^n {{A_j}} }} = \left\{ {\begin{array}{*{20}{c}}{f\left( x \right),}&{x \in {A_n}} \\ {0,}&{x \notin {A_n}}\end{array}} \right.##

where the nesting property has been used. Also let ##f: = f \circ {\chi _A} = \left\{ {\begin{array}{*{20}{c}}{f\left( x \right),}&{x \in A} \\ {0,}&{x \notin A}\end{array}} \right.##

Then $${f_1}\left( x \right) \geq {f_2}\left( x \right) \geq  \cdots  \geq {f_n}\left( x \right) \geq {f_{n + 1}}\left( x \right) \geq  \cdots  \geq f\left( x \right)$$

hence by the Lebesgue Dominated Convergence Theorem with $${f_1}\left( x \right) \geq \left| {{f_n}\left( x \right)} \right|\,,\forall x \in {\mathbb{R}^n},\forall n \in {\mathbb{Z}^ + }$$

we have

$$\mathop {\lim }\limits_{n \to \infty } \,\phi \left( {{A_n}} \right) = \mathop {\lim }\limits_{n \to \infty } \,\int_{{A_n}} {fd\mu }  = \int_A {fd\mu }  = \phi \left( A \right)$$

the required result.

A Needed Limit 3.3:

We’ll use this result a lot, nearly every problem, so here it goes:

3.3) Use the Euler product form of the gamma function to show that ##\mathop {\lim }\limits_{N \to \infty } {{{\Gamma ^n}\left( {1 + \frac{k}{N}} \right)} \mathord{\left/ {\vphantom {{{\Gamma ^n}\left( {1 + \frac{k}{N}} \right)} {\Gamma \left( {1 + \frac{{kn}}{N}} \right)}}} \right. } {\Gamma \left( {1 + \frac{{kn}}{N}} \right)}} = 1## .

$$\begin{gathered}\mathop {\lim }\limits_{N \to \infty } \tfrac{{{\Gamma ^n}\left( {1 + \tfrac{k}{N}} \right)}}{{\Gamma \left( {1 + \tfrac{{kn}}{N}} \right)}} = \mathop {\lim }\limits_{N \to \infty } \tfrac{{{{\left( {1 + \tfrac{k}{N}} \right)}^{ – n}}\prod\limits_{\lambda  = 1}^\infty  {\tfrac{{{{\left( {1 + \tfrac{1}{\lambda }} \right)}^{n\left( {1 + \tfrac{k}{N}} \right)}}}}{{{{\left( {1 + \tfrac{{1 + \tfrac{{kn}}{N}}}{\lambda }} \right)}^n}}}} }}{{{{\left( {1 + \tfrac{{kn}}{N}} \right)}^{ – 1}}\prod\limits_{j = 1}^\infty  {\tfrac{{{{\left( {1 + \tfrac{1}{j}} \right)}^{1 + \tfrac{{kn}}{N}}}}}{{\left( {1 + \tfrac{{1 + \tfrac{{kn}}{N}}}{j}} \right)}}} }} \\ = \mathop {\lim }\limits_{N \to \infty } {\left( {1 + \tfrac{k}{N}} \right)^{ – n}}\left( {1 + \tfrac{{kn}}{N}} \right)\prod\limits_{\lambda  = 1}^\infty  {\left[ {\tfrac{{{{\left( {1 + \tfrac{1}{\lambda }} \right)}^{n – 1}}\left( {1 + \tfrac{{1 + \tfrac{{kn}}{N}}}{\lambda }} \right)}}{{{{\left( {1 + \tfrac{{1 + \tfrac{k}{N}}}{\lambda }} \right)}^n}}}} \right]}  \\ = \prod\limits_{\lambda  = 1}^\infty  {\left[ {{{\left( {1 + \tfrac{1}{\lambda }} \right)}^{n – 1}}\mathop {\lim }\limits_{N \to \infty } \tfrac{{\left( {1 + \tfrac{{1 + \tfrac{{kn}}{N}}}{\lambda }} \right)}}{{{{\left( {1 + \tfrac{{1 + \tfrac{k}{N}}}{\lambda }} \right)}^n}}}} \right]}  \\ = \prod\limits_{\lambda  = 1}^\infty  {\left[ {{{\left( {1 + \tfrac{1}{\lambda }} \right)}^{n – 1}}\tfrac{{\left( {1 + \tfrac{1}{\lambda }} \right)}}{{{{\left( {1 + \tfrac{1}{\lambda }} \right)}^n}}}} \right]}  = 1 \\ \end{gathered}$$

Example 3.4: Content of the Orthotope

As an example of Theorem 4.2 consider the orthotope $${S^{n\left(  +  \right)}}: = \bigcap\limits_{j = 1}^\infty  {S_j^{n\left(  +  \right)}} $$ where we define $$S_N^{n\left(  +  \right)}: = \left\{ {\vec x \in {\mathbb{R}^n}|{x_i} \geq 0\forall i,\sum\limits_{k = 1}^n {{{\left( {\frac{{{x_k}}}{{{b_k}}}} \right)}^{2N}}}  \leq n} \right\}$$

Note that by lemma 2.1 ##S_N^{n\left(  +  \right)}## and ##{S^{n\left(  +  \right)}}## satisfy the nesting property in the hypotheses of theorem 2.2 so that we can evaluate the content integral by corollary 1.2,

$$\begin{gathered}{\text{content}}\left( {{S^{n\left(  +  \right)}}} \right) = \mathop {\lim }\limits_{N \to \infty } \,\iint {\mathop  \cdots \limits_{S_N^{n\left(  +  \right)}} \int {d{z_n} \ldots d{z_2}d{z_1}} } \\ = \mathop {\lim }\limits_{N \to \infty } \,\left\{ {{{{n^{\sum\limits_{k = 1}^n {\tfrac{1}{{2N}}} }}\prod\limits_{q = 1}^n {\left[ {\frac{{{b_p}}}{{2N}}\Gamma \left( {\frac{1}{{2N}}} \right)} \right]} } \mathord{\left/{\vphantom {{{n^{\sum\limits_{k = 1}^n {\tfrac{1}{{2N}}} }}\prod\limits_{q = 1}^n {\left[ {\frac{{{b_p}}}{{2N}}\Gamma \left( {\frac{1}{{2N}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\frac{1}{{2N}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\frac{1}{{2N}}} } \right)}}} \right\} \\ = \mathop {\lim }\limits_{N \to \infty } \,\left[ {{n^{\tfrac{n}{{2N}}}}\tfrac{{{\Gamma ^n}\left( {\frac{1}{{2N}}} \right)\prod\limits_{q = 1}^n {{b_p}} }}{{{{\left( {2N} \right)}^n}\Gamma \left( {1 + \tfrac{n}{{2N}}} \right)}}} \right] = \prod\limits_{q = 1}^n {\left( {{b_p}} \right) \cdot } \underbrace {\mathop {\lim }\limits_{N \to \infty } \,\left( {{n^{\tfrac{n}{{2N}}}}} \right)}_{ = {n^0}} \cdot \underbrace {\mathop {\lim }\limits_{N \to \infty } \left[ {\tfrac{{{\Gamma ^n}\left( {1 + \frac{1}{{2N}}} \right)}}{{\Gamma \left( {1 + \tfrac{n}{{2N}}} \right)}}} \right]}_{ = 1{\text{ Limit 3.3}}} = \prod\limits_{q = 1}^n {{b_p}}  \\ \end{gathered}$$

as it must.

Example 3.4: The Zeta Function

Show that $$Z\left( n \right): = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{k = 1}^n {{x_k}} } \right)}^{ – 1}}d{x_n} \ldots d{x_2}d{x_1}} } }  = \zeta \left( n \right)\forall n \in {\mathbb{Z}^ + } – \left\{ 1 \right\}$$

where ##\zeta \left( {\, \cdot \,} \right)## is the Riemann zeta function. The domain of integration is a unit hypercube with one vertex at the origin and the vertex which is farthest from said point is at ##\left( {1,1, \ldots ,1} \right)## suggesting the use of the sequence of sets here defined throughout the remnant of this Insight $$C_N^n: = \left\{ {\vec x \in {\mathbb{R}^n}|{x_i} \geq 0\forall i,\sum\limits_{k = 1}^n {x_k^{2N}}  \leq n – 1} \right\}$$ and also define the set ##{C^n}: = \bigcap\limits_{j = 1}^\infty  {C_j^n} ##. Then we have

$$\begin{gathered}Z\left( n \right) = \mathop {\lim }\limits_{N \to \infty } \,\int {\int_{C_N^n} { \cdots \int {\tfrac{{\prod\nolimits_{i = 1}^n {d{x_i}} }}{{1 – \prod\nolimits_{k = 1}^n {{x_k}} }}} } }  = \mathop {\lim }\limits_{N \to \infty } \,\int {\int_{C_N^n} { \cdots \int {\sum\limits_{k = 1}^\infty  {\prod\limits_{i = 1}^n {\left( {x_i^{k – 1}d{x_i}} \right)} } } } }  \\ = \mathop {\lim }\limits_{N \to \infty } \,\sum\limits_{k = 1}^\infty  {\int {\int_{C_N^n} { \cdots \int {\prod\limits_{i = 1}^n {\left( {x_i^{k – 1}d{x_i}} \right)} } } } }  \\ = \mathop {\lim }\limits_{N \to \infty } \,\sum\limits_{k = 1}^\infty  {{{\left( {n – 1} \right)}^{\sum\limits_{p = 1}^n {\frac{k}{{2N}}} }}{{\prod\limits_{q = 1}^n {\left[ {\frac{{{1^k}}}{{2N}}\Gamma \left( {\frac{k}{{2N}}} \right)} \right]} } \mathord{\left/ {\vphantom {{\prod\limits_{q = 1}^n {\left[ {\frac{{{1^k}}}{{2N}}\Gamma \left( {\frac{k}{{2N}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{i = 1}^n {\frac{k}{{2N}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{i = 1}^n {\frac{k}{{2N}}} } \right)}}} \\ = \mathop {\lim }\limits_{N \to \infty } \,\left\{ {\sum\limits_{k = 1}^\infty  {\left[ {{{\left( {n – 1} \right)}^{\tfrac{{nk}}{{2N}}}} \cdot \tfrac{1}{{{k^n}}} \cdot \tfrac{{{\Gamma ^n}\left( {1 + \tfrac{k}{{2N}}} \right)}}{{\Gamma \left( {1 + \tfrac{{nk}}{{2N}}} \right)}}} \right]} } \right\} \\ = \sum\limits_{k = 1}^\infty  {\tfrac{1}{{{k^n}}} \cdot \underbrace {\mathop {\lim }\limits_{N \to \infty } \,{{\left( {n – 1} \right)}^{\tfrac{{nk}}{{2N}}}}}_{ = {{\left( {n – 1} \right)}^0}} \cdot \underbrace {\mathop {\lim }\limits_{N \to \infty } \,\tfrac{{{\Gamma ^n}\left( {1 + \tfrac{k}{{2N}}} \right)}}{{\Gamma \left( {1 + \tfrac{{nk}}{{2N}}} \right)}}}_{ = 1{\text{ Limit 3.3}}}}  = \sum\limits_{k = 1}^\infty  {\tfrac{1}{{{k^n}}}}  = \zeta \left( n \right) \\ \end{gathered}$$

This was a well-known integral, but likely demonstrated a new way to achieve a known result. We shall use this technique of evaluating improper multiple integrals over the unit hypercube on many functions in this section. But first,

An alternate evaluation of the above example:

$$\begin{gathered}Z\left( n \right) = \int {\int_{{C^n}} { \cdots \int {\tfrac{{\prod\nolimits_{i = 1}^n {d{x_i}} }}{{1 – \prod\nolimits_{k = 1}^n {{x_k}} }}} } }  = \int {\int_{{C^{n – 1}}} { \cdots \int {\ln \left( {\tfrac{1}{{1 – \prod\nolimits_{k = 1}^{n – 1} {{x_k}} }}} \right) \cdot \prod\limits_{i = 1}^{n – 1} {\tfrac{{d{x_i}}}{{{x_i}}}} } } }  \\ = \int {\int_{{C^{n – 1}}} { \cdots \int {\ln \left[ {\prod\limits_{q = 0}^\infty  {\left( {1 + \prod\limits_{k = 1}^{n – 1} {x_k^{{2^q}}} } \right)} } \right] \cdot \prod\limits_{i = 1}^{n – 1} {\tfrac{{d{x_i}}}{{{x_i}}}} } } }  \\ = \sum\limits_{q = 0}^\infty  {\int {\int_{{C^{n – 1}}} { \cdots \int {\ln \left( {1 + \prod\limits_{k = 1}^{n – 1} {x_k^{{2^q}}} } \right) \cdot \prod\limits_{i = 1}^{n – 1} {\tfrac{{d{x_i}}}{{{x_i}}}} } } } }  = \mathop {\lim }\limits_{N \to \infty } \,\sum\limits_{q = 0}^\infty  {\sum\limits_{k = 1}^\infty  {\tfrac{{{{\left( { – 1} \right)}^{k – 1}}}}{k}\int {\int_{C_N^{n – 1}} { \cdots \int {\prod\limits_{k = 1}^{n – 1} {x_k^{k{2^q} – 1}d{x_k}} } } } } }  \\ = \mathop {\lim }\limits_{N \to \infty } \,\sum\limits_{q = 0}^\infty  {\sum\limits_{k = 1}^\infty  {\tfrac{{{{\left( { – 1} \right)}^{k – 1}}}}{k}{{\left( {n – 2} \right)}^{\sum\limits_{p = 1}^n {\frac{{k{2^q}}}{{2N}}} }}{{\prod\limits_{i = 1}^{n – 1} {\left[ {\frac{1}{{2N}}\Gamma \left( {\frac{{k{2^q}}}{{2N}}} \right)} \right]} } \mathord{\left/ {\vphantom {{\prod\limits_{i = 1}^{n – 1} {\left[ {\frac{1}{{2N}}\Gamma \left( {\frac{{k{2^q}}}{{2N}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{j = 1}^{n – 1} {\frac{{k{2^q}}}{{2N}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{j = 1}^{n – 1} {\frac{{k{2^q}}}{{2N}}} } \right)}}} }  \\ = \sum\limits_{q = 0}^\infty  {\sum\limits_{k = 1}^\infty  {\tfrac{{{{\left( { – 1} \right)}^{k – 1}}}}{{{k^n}{2^{\left( {n – 1} \right)q}}}} \cdot \underbrace {\mathop {\lim }\limits_{N \to \infty } \,{{\left( {n – 2} \right)}^{\frac{{\left( {n – 1} \right)k{2^q}}}{{2N}}}}}_{ = {{\left( {n – 2} \right)}^0}} \cdot \underbrace {\mathop {\lim }\limits_{N \to \infty } \,\tfrac{{{\Gamma ^{n – 1}}\left( {1 + \frac{{k{2^q}}}{{2N}}} \right)}}{{\Gamma \left( {1 + \tfrac{{\left( {n – 1} \right)k{2^q}}}{{2N}}} \right)}}}_{ = 1{\text{ Limit 3.3}}}} } \\  = \sum\limits_{q = 0}^\infty  {\sum\limits_{k = 1}^\infty  {\tfrac{{{{\left( { – 1} \right)}^{k – 1}}}}{{{k^n}}} \cdot {{\left( {\tfrac{1}{{{2^{n – 1}}}}} \right)}^q}} }  = \sum\limits_{k = 1}^\infty  {\left[ {\tfrac{{{{\left( { – 1} \right)}^{k – 1}}}}{{{k^n}}}\sum\limits_{q = 0}^\infty  {{{\left( {\tfrac{1}{{{2^{n – 1}}}}} \right)}^q}} } \right]}  \\ = {\left( {1 – {2^{1 – n}}} \right)^{ – 1}}\sum\limits_{k = 1}^\infty  {\tfrac{{{{\left( { – 1} \right)}^{k – 1}}}}{{{k^n}}}}  = \sum\limits_{k = 1}^\infty  {\tfrac{1}{{{k^n}}}}  = \zeta \left( n \right) \\ \end{gathered}$$

The reader may use this technique of evaluating multiple integrals over the unit hypercube to verify the following 

Summary of Functions Represented as Multiple Integrals Over the Unit Hypercube:

The Lerch Transcendent: ##\Phi \left( {z,n,y} \right): = \sum\limits_{q = 0}^\infty  {\frac{{{z^q}}}{{{{\left( {q + y} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – z\prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {\lambda _k^{y – 1}d{\lambda _k}} } } } }##

Legendre Chi Function: ##{\chi _n}\left( z \right): = \sum\limits_{q = 0}^\infty  {\frac{{{z^{2q + 1}}}}{{{{\left( {2q + 1} \right)}^n}}} = z\int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – {z^2}\prod\limits_{q = 1}^n {\lambda _q^2} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

Polygamma Function: ##{\psi _n}\left( z \right): = \sum\limits_{q = 0}^\infty  {\frac{{{{\left( { – 1} \right)}^{n + 1}}n!}}{{{{\left( {z + q} \right)}^{n + 1}}}} = {{\left( { – 1} \right)}^{n + 1}}n!\int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^{n + 1} {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^{n + 1} {\lambda _k^{z – 1}d{\lambda _k}} } } } }##

Polylogarithm of Order n: ##{\text{L}}{{\text{i}}_n}\left( z \right): = \sum\limits_{q = 1}^\infty  {\frac{{{z^q}}}{{{q^n}}} = z\int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – z\prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

Hurwitz Zeta Function: ##\zeta \left( {n,z} \right): = \sum\limits_{q = 0}^\infty  {\frac{1}{{{{\left( {q + z} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {\lambda _k^{z – 1}d{\lambda _k}} } } } }##

Riemann Zeta Function: ##\zeta \left( n \right): = \sum\limits_{q = 1}^\infty  {\frac{1}{{{q^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

Dirichlet Beta Function: ##\beta \left( n \right): = \sum\limits_{q = 0}^\infty  {\frac{{{{\left( { – 1} \right)}^q}}}{{{{\left( {2q + 1} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 + \prod\limits_{q = 1}^n {\lambda _q^2} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

Dirichlet Eta Function: ##\eta \left( n \right): = \sum\limits_{q = 1}^\infty  {\frac{{{{\left( { – 1} \right)}^{q – 1}}}}{{{q^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 + \prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

Dirichlet Lambda Function: ##\lambda \left( n \right): = \sum\limits_{q = 0}^\infty  {\frac{1}{{{{\left( {2q + 1} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^n {\lambda _q^2} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

Exercises

1) Verify the remaining unit hypercube integral identities from the above summary.

Answers to Exercises – Unit Hypercube Integrals

1) Verify the remaining unit hypercube integral identities from the above summary.

a) The Lerch Transcendent: ##\Phi \left( {z,n,y} \right): = \sum\limits_{q = 0}^\infty  {\frac{{{z^q}}}{{{{\left( {q + y} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – z\prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {\lambda _k^{y – 1}d{\lambda _k}} } } } }##

$$\begin{eqnarray*}\Phi ( z,n,y ) &=& \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – z\prod\limits_{q = 1}^n \lambda _q \right) ^{ – 1}\prod\limits_{k = 1}^n \lambda _k^{y – 1}d{\lambda _k} \\ &=& \lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n}} \int \sum\limits_{k=0}^\infty z^k\prod\limits_{q = 1}^n \lambda _q^{k+y-1}d{\lambda _q}  \\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \Phi \left( {z,n,y} \right)  &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty z^k {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{k+y}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{k+y}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{k+y}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{k+y}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{k+y}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{k+y}}}{{{2N}}}} }}}_{=1}\sum\limits_{k=0}^\infty z^k {{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{k+y}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{k+y}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(k+y)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(k+y)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty z^k  \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(k+y)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{k+y}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(k+y)^n}\Gamma ^n\left( \tfrac{k+y}{2N} \right)  } \Gamma \left( 1 +\tfrac{(k+y)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3} } \\  &=&  \sum\limits_{k=0}^\infty   \tfrac{z^k}{(k+y)^n} \\ \end{eqnarray*}$$

b) Legendre Chi Function: ##\chi _n ( z ) = z \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – z^2\prod\limits_{q = 1}^n \lambda _q^2 \right) ^{ – 1} \prod\limits_{k = 1}^n d{\lambda _k} ##

$$\begin{eqnarray*}\chi _n ( z ) &=& z\int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – z^2\prod\limits_{q = 1}^n \lambda _q^2 \right) ^{ – 1}\prod\limits_{k = 1}^n d{\lambda _k} \\ &=& z\lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n} \int \sum\limits_{k=0}^\infty z^{2k}\prod\limits_{q = 1}^n \lambda _q^{2k}d{\lambda _q} } \\ &=& z\lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty z^{2k}\iint {\mathop  \cdots \limits_{C_N^n} \int \prod\limits_{q = 1}^n \lambda _q^{2k}d{\lambda _q} }\\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \chi _n \left( z \right)  &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty z^{2k+1} {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} }}}_{=1}\sum\limits_{k=0}^\infty z^{2k+1}{{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(2k+1)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(2k+1)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty z^{2k+1}  \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(2k+1)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{2k+1}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(2k+1)^n}\Gamma ^n\left( \tfrac{2k+1}{2N} \right)  } \Gamma \left( 1 +\tfrac{(2k+1)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{k=0}^\infty   \tfrac{z^{2k+1}}{(2k+1)^n} \\ \end{eqnarray*}$$

c) Polygamma Function: ##{\psi _n}\left( z \right): = \sum\limits_{q = 0}^\infty  {\frac{{{{\left( { – 1} \right)}^{n + 1}}n!}}{{{{\left( {z + q} \right)}^{n + 1}}}} = {{\left( { – 1} \right)}^{n + 1}}n!\int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^{n + 1} {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^{n + 1} {\lambda _k^{z – 1}d{\lambda _k}} } } } }##

$$\begin{eqnarray*}\psi _n ( z ) &=& (-1)^{n+1}n! \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – \prod\limits_{q = 1}^{n+1} \lambda _q \right) ^{ – 1}\prod\limits_{k = 1}^{n+1}\lambda_k^{z-1} d{\lambda _k} \\ &=& (-1)^{n+1}n! \lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty\iint {\mathop  \cdots \limits_{C_N^{n+1}} \int  \prod\limits_{q = 1}^{n+1} \lambda _q^{z+k-1}d{\lambda _q} } \\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \psi _n \left( z \right)  &=& (-1)^{n+1}n!\lim\limits_{N\to\infty} \sum\limits_{q=0}^\infty  {n^{\sum\limits_{p = 1}^{n+1} {\tfrac{{{z+q}}}{{{2N}}}} }}{{\prod\limits_{k = 1}^{n+1} {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{z+q}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{k = 1}^{n+1} {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{z+q}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{\lambda = 1}^{n+1} {\tfrac{{{z+q}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{\lambda = 1}^n {\tfrac{{{z+q}}}{{{2N}}}} } \right)}} \\ &=& (-1)^{n+1}n!\lim\limits_{N\to\infty} \underbrace{{n^{\sum\limits_{p = 1}^{n+1} {\tfrac{{{z+q}}}{{{2N}}}} }}}_{=n^0}\sum\limits_{q=0}^\infty \tfrac{{(2N)^{n+1}}}{(z+q)^{n+1}}\cdot{{ {{\tfrac{{1}}{{{(2N)^{n+1}}}}\Gamma ^{n+1}\left( {1+\tfrac{{{z+q}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{(2N)^{n+1}}}{(z+q)^{n+1}}\cdot\tfrac{{1}}{{{(2N)^{n+1}}}}\Gamma ^{n+1}\left( {1+\tfrac{{{z+q}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(2k+1)(n+1)}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(z+q)(n+1)}}}{{{2N}}}} } \right)}} \\ &=& (-1)^{n+1}n!\lim\limits_{N\to\infty} \sum\limits_{q=0}^\infty  \tfrac{1}{(z+q)^{n+1}} \underbrace{\Gamma ^{n+1}\left(   1 + \tfrac{z+q}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(z+q)^{n+1}}\Gamma ^{n+1}\left( 1+\tfrac{z+q}{2N} \right)  } \Gamma \left( 1 +\tfrac{(z+q)(n+1)}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{q=0}^\infty   \tfrac{(-1)^{n+1}n!}{(z+q)^{n+1}} \\ \end{eqnarray*}$$

d) Polylogarithm of Order n: ##{\text{L}}{{\text{i}}_n}\left( z \right): = \sum\limits_{q = 1}^\infty  {\frac{{{z^q}}}{{{q^n}}} = z\int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – z\prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

$$\begin{eqnarray*}{\text{L}}{{\text{i}}_n} ( z )  &=& z\int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – z\prod\limits_{q = 1}^n \lambda _q \right) ^{ – 1}\prod\limits_{k = 1}^n d{\lambda _k} \\ &=& z\lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n} \int \sum\limits_{k=0}^\infty z^{k}\prod\limits_{q = 1}^n \lambda _q^{k}d{\lambda _q} } \\ &=& \lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty z^{k+1}\iint {\mathop  \cdots \limits_{C_N^n} \int \prod\limits_{q = 1}^n \lambda _q^{k}d{\lambda _q} }\\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} {\text{L}}{{\text{i}}_n} ( z )  &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty z^{k+1} {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{k+1}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{k+1}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} }}}_{=n^0}\sum\limits_{k=0}^\infty z^{k+1}{{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{k+1}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{k+1}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(k+1)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(k+1)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty z^{k+1}  \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(k+1)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{k+1}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(k+1)^n}\Gamma ^n\left( \tfrac{k+1}{2N} \right)  } \Gamma \left( 1 +\tfrac{(k+1)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{k=1}^\infty   \tfrac{z^k}{k^n} \\ \end{eqnarray*}$$

e) Hurwitz Zeta Function: ##\zeta \left( {n,z} \right): = \sum\limits_{q = 0}^\infty  {\frac{1}{{{{\left( {q + z} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {\lambda _k^{z – 1}d{\lambda _k}} } } } }##

$$\begin{eqnarray*}\zeta \left( {n,z} \right) &=& \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – \prod\limits_{q = 1}^n \lambda _q \right) ^{ – 1}\prod\limits_{k = 1}^n \lambda_k^{z-1} d{\lambda _k} \\ &=& \lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n} \int \sum\limits_{k=0}^\infty \prod\limits_{q = 1}^n \lambda _q^{z+k-1}d{\lambda _q} } \\ &=& \lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty \iint {\mathop  \cdots \limits_{C_N^n} \int \prod\limits_{q = 1}^n \lambda _q^{z+k-1}d{\lambda _q} }\\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \zeta \left( {n,z} \right)  &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{z+k}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{z+k}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{z+k}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{z+k}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{z+k}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{z+k}}}{{{2N}}}} }}}_{=n^0}\sum\limits_{k=0}^\infty {{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{z+k}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{z+k}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(z+k)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(z+k)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty  \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(z+k)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{z+k}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(z+k)^n}\Gamma ^n\left( \tfrac{z+k}{2N} \right)  } \Gamma \left( 1 +\tfrac{(z+k)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{k=1}^\infty   \tfrac{1}{(z+k)^n} \\ \end{eqnarray*}$$

f) Dirichlet Beta Function: ##\beta ( n ) : = \sum\limits_{q = 0}^\infty  {\frac{{{{\left( { – 1} \right)}^q}}}{{{{\left( {2q + 1} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 + \prod\limits_{q = 1}^n {\lambda _q^2} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

$$\begin{eqnarray*}\beta ( n ) &=& \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 + \prod\limits_{q = 1}^n \lambda _q^2\right) ^{ – 1}\prod\limits_{k = 1}^n d{\lambda _k} \\ &=& \lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n} \int \sum\limits_{k=0}^\infty (-1)^k\prod\limits_{q = 1}^n \lambda _q^{2k}d{\lambda _q} } \\ &=& \lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty (-1)^k \iint {\mathop  \cdots \limits_{C_N^n} \int \prod\limits_{q = 1}^n \lambda _q^{2k}d{\lambda _q} }\\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \beta ( n ) &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty (-1)^k {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} }}}_{=n^0}\sum\limits_{k=0}^\infty (-1)^k {{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(2k+1)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(2k+1)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty (-1)^k \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(2k+1)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{2k+1}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(2k+1)^n}\Gamma ^n\left( \tfrac{2k+1}{2N} \right)  } \Gamma \left( 1 +\tfrac{(2k+1)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{k=0}^\infty   \tfrac{(-1)^k}{(2k+1)^n} \\ \end{eqnarray*}$$

g) Dirichlet Eta Function: ##\eta \left( n \right): = \sum\limits_{q = 1}^\infty  {\frac{{{{\left( { – 1} \right)}^{q – 1}}}}{{{q^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 + \prod\limits_{q = 1}^n {{\lambda _q}} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

$$\begin{eqnarray*}\eta ( n ) &=& \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 + \prod\limits_{q = 1}^n \lambda _q\right) ^{ – 1}\prod\limits_{k = 1}^n d{\lambda _k} \\ &=& \lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n} \int \sum\limits_{k=0}^\infty (-1)^k\prod\limits_{q = 1}^n \lambda _q^{k}d{\lambda _q} } \\ &=& \lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty (-1)^k \iint {\mathop  \cdots \limits_{C_N^n} \int \prod\limits_{q = 1}^n \lambda _q^{k}d{\lambda _q} }\\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \eta ( n ) &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty (-1)^k {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{k+1}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{k+1}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{k+1}}}{{{2N}}}} }}}_{=n^0}\sum\limits_{k=0}^\infty (-1)^k {{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{k+1}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{k+1}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(k+1)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(k+1)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty (-1)^k \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(k+1)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{k+1}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(k+1)^n}\Gamma ^n\left( \tfrac{k+1}{2N} \right)  } \Gamma \left( 1 +\tfrac{(k+1)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{k=1}^\infty   \tfrac{(-1)^{k-1}}{k^n} \\ \end{eqnarray*}$$

h) Dirichlet Lambda Function: ##\lambda \left( n \right): = \sum\limits_{q = 0}^\infty  {\frac{1}{{{{\left( {2q + 1} \right)}^n}}} = \int_0^1 {\int_0^1 { \cdots \int_0^1 {{{\left( {1 – \prod\limits_{q = 1}^n {\lambda _q^2} } \right)}^{ – 1}}\prod\limits_{k = 1}^n {d{\lambda _k}} } } } }##

$$\begin{eqnarray*}\lambda ( n ) &=& \int_0^1 \int_0^1  \cdots \int_0^1 \left( 1 – \prod\limits_{q = 1}^n \lambda _q^2\right) ^{ – 1}\prod\limits_{k = 1}^n d{\lambda _k} \\ &=& \lim\limits_{N\to\infty}\iint {\mathop  \cdots \limits_{C_N^n} \int \sum\limits_{k=0}^\infty \prod\limits_{q = 1}^n \lambda _q^{2k}d{\lambda _q} } \\ &=& \lim\limits_{N\to\infty}\sum\limits_{k=0}^\infty  \iint {\mathop  \cdots \limits_{C_N^n} \int \prod\limits_{q = 1}^n \lambda _q^{2k}d{\lambda _q} }\\ \end{eqnarray*}$$

Then by Theorem 1.1, we have

$$\begin{eqnarray*} \lambda ( n ) &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty  {(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} }}{{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} \right]} } \mathord{\left/{\vphantom {{\prod\limits_{q = 1}^n {\left[ {\tfrac{{1}}{{{2N}}}\Gamma \left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} \right]} } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 + \sum\limits_{k = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \underbrace{{(n-1)^{\sum\limits_{p = 1}^n {\tfrac{{{2k+1}}}{{{2N}}}} }}}_{=n^0}\sum\limits_{k=0}^\infty {{ {{\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)}} } \mathord{\left/{\vphantom {{ { {\tfrac{{1}}{{{(2N)^n}}}\Gamma ^n\left( {\tfrac{{{2k+1}}}{{{2N}}}} \right)} } } {\Gamma \left( {1 +{\tfrac{{{(2k+1)n}}}{{{2N}}}} } \right)}}} \right. } {\Gamma \left( {1 +  {\tfrac{{{(2k+1)n}}}{{{2N}}}} } \right)}} \\ &=& \lim\limits_{N\to\infty} \sum\limits_{k=0}^\infty  \tfrac{1}{(2N)^n} \cdot\tfrac{(2N)^n}{(2k+1)^n} \underbrace{\Gamma ^n\left(   1+ \tfrac{2k+1}{2N} \right) \mathord{\left/{\vphantom {\tfrac{1}{(2N)^n}\cdot\tfrac{(2N)^n}{(2k+1)^n}\Gamma ^n\left( \tfrac{2k+1}{2N} \right)  } \Gamma \left( 1 +\tfrac{(2k+1)n}{2N}  \right) } \right. }  }_{ =1 \text{ Limit 3.3 } } \\  &=&  \sum\limits_{k=0}^\infty   \tfrac{1}{(2k+1)^n} \\ \end{eqnarray*}$$