- #1
simphys
- 322
- 45
- Homework Statement
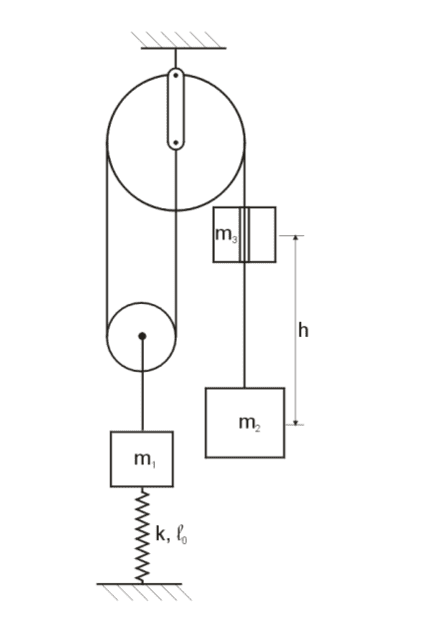
- 1. Two masses m1 and m2 are situated in a system with ideal pulleys as shown in the
figure. This system is in the vertical plane. A spring (constant k, rest length l0)
connects mass m1 with the ground.
Data: m1= 1.5 kg, m2 = 2 kg, m3= 1.5 kg, k = 50 N/m, ##l_0##= 0.4 m, h= 2 m.
a) The system is in rest at t = 0 s. Determine at that instance the tension in all
the ropes and the compression/extension of the spring.
b) Then, an extra mass m3 is dropped from a height h, hits mass m2 and sticks to
that mass. During this very short impact, the spring does not exert an impulse.
Determine the velocities of all the masses in the system right after the impact
and also the impulses exerted by the ropes.
c) How much energy was lost during the impact?
d) Determine the accelerations of all the masses right after the impact.
- Relevant Equations
- cons of energy, momentum, relative motion,....
Hello there, can I get some help with (b) please?
first of all I wanted to ask.. can is it permitted to use different systems in one exercises?
like f.e. for conservation of energy to find the velocity of ##m_3## I used as system only ##m_3## but for the collision I used the 3 masses as the system.
So what I need is one more equation which I can't find...
my work:
Conservation of energy (system = ##m_3##):
##0 = \frac12 * m_3 * v_3^2 - m_3 gh##
-> ##v_3 = \sqrt(2 * 9.81 * 2)## = ##6.264 \frac ms##
then for the collision: system = all 3 masses
## -m_3v_3 + J_T = -(m_2 + m_3)v' + m_1v'_1## impuls from gravity neglected and impuls from spring not accounted for as stated. Then getting another eq. from absolute dependant motion from the rope, we get:
##2s_1 + s' = l## with s' being the position from the fixed pulley to the combination of mass 2 and 3 and ##s_1## being the positoin for the pulley where ##m_1## is attached.
-> ##2v_1 + v' = 0 ## --> ##v' = -2v_1##
This gives me three equations.
Can someone give me a tip on the fourth one please? Thanks in advance.
edit: I was thinking about relative motion or conservation of energy after the collision, but can't see how it'll apply as I'll introduce new unkowns.

first of all I wanted to ask.. can is it permitted to use different systems in one exercises?
like f.e. for conservation of energy to find the velocity of ##m_3## I used as system only ##m_3## but for the collision I used the 3 masses as the system.
So what I need is one more equation which I can't find...
my work:
Conservation of energy (system = ##m_3##):
##0 = \frac12 * m_3 * v_3^2 - m_3 gh##
-> ##v_3 = \sqrt(2 * 9.81 * 2)## = ##6.264 \frac ms##
then for the collision: system = all 3 masses
## -m_3v_3 + J_T = -(m_2 + m_3)v' + m_1v'_1## impuls from gravity neglected and impuls from spring not accounted for as stated. Then getting another eq. from absolute dependant motion from the rope, we get:
##2s_1 + s' = l## with s' being the position from the fixed pulley to the combination of mass 2 and 3 and ##s_1## being the positoin for the pulley where ##m_1## is attached.
-> ##2v_1 + v' = 0 ## --> ##v' = -2v_1##
This gives me three equations.
Can someone give me a tip on the fourth one please? Thanks in advance.
edit: I was thinking about relative motion or conservation of energy after the collision, but can't see how it'll apply as I'll introduce new unkowns.