- #1
BiGyElLoWhAt
Gold Member
- 1,622
- 131
Hi,
I'm trying to come up with a section of an optics based physics lab designed for 2nd year Calc-based college students. Calc 2 is a co-req.
There are 2 labs that are intimately linked together. The first effectively revolves around taking ##d_i(d_o)## data from a lens, source and screen system, then plotting in excel.
I'm trying to come up with an intuitive way to linearize the data. Students tend to not get a lot of data analysis, particularly in early labs, so I'm trying to add this in while I have the opportunity.
The end goal is to get to the relation ##d_i = \frac{fd_o}{d_o-f}##.
My thoughts are this:
Give a little background, note that if I have some data that looks like a particular function, I can plot against that function to check to see if it matches, i.e. e^x vs. e^x is a line with slope 1 and intercept 0.
Give a few options for possible "general fits": 1/x, e^-x, maybe 1 or two more?
Student data should have both vertical and horizontal asymptotes at f. This rules out e^-x, as it only goes to inf at x=>-inf.
With 1/x hopefully chosen, now we can fix the vertical asymptote by shifting from x-> x-f.
We now have ##\frac{1}{x-f}##, which has a vertical asymptote at f, but horizontal at 0.
Now here is a fork that I'm trying to remedy.
Occam's razor suggests that we should add f, which will fix the horizontal asymptote. It does. So does multiplying by f*x, i.e. ##\frac{fx}{x-f}##. If I follow Occam's razor and plot this function vs. my data, I get a very linear graph with a slope of 2 and y intercept of around -f. This implies that we can add f and multiply by 1/2 to get a good fit. It works, really well, actually. All the data points are within around a centimeter of using the correct fit.
I will attach all 3 graphs with the equations. I added in a bit of random variance to the ##d_i## measurements, so they are all +/- 1cm.
I would really like to end this section by arriving at ##1/f = 1/d_o + 1/d_i##
Any ideas on adjustments that could be made, or why we can/should argue around the "add f" method?
The 3 labeled graphs are as follows:
Correct Fit = ##d_i## vs ##\frac{fd_o}{d_o-f}## which can be arranged into the standard thin lens equation.
Add f = ##d_i## vs ##\frac{1}{d_o-f} + f##
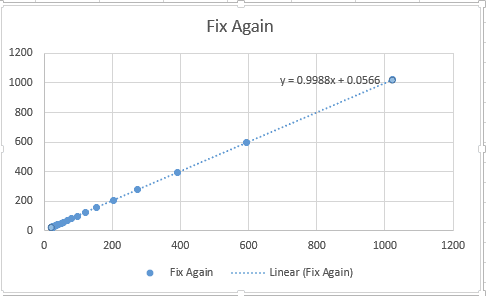
Fix again = ##d_i## vs ##\frac{1}{2}(\frac{1}{d_o-f} + 2f)## , I added f again to fix the intercept, then multiplied by 1/2 to fix the slope.

If need be, I can attach the spreadsheet.
Any ideas or suggestions are appreciated.
What I find really interesting is that the correct fit and fix again trendlines are both very convincing, although correct is objectively ever so slightly better, and over a large data range at that. Horizontal axis is fit values, vertical is simulated data with random variance.
All plots use the same data.
I'm trying to come up with a section of an optics based physics lab designed for 2nd year Calc-based college students. Calc 2 is a co-req.
There are 2 labs that are intimately linked together. The first effectively revolves around taking ##d_i(d_o)## data from a lens, source and screen system, then plotting in excel.
I'm trying to come up with an intuitive way to linearize the data. Students tend to not get a lot of data analysis, particularly in early labs, so I'm trying to add this in while I have the opportunity.
The end goal is to get to the relation ##d_i = \frac{fd_o}{d_o-f}##.
My thoughts are this:
Give a little background, note that if I have some data that looks like a particular function, I can plot against that function to check to see if it matches, i.e. e^x vs. e^x is a line with slope 1 and intercept 0.
Give a few options for possible "general fits": 1/x, e^-x, maybe 1 or two more?
Student data should have both vertical and horizontal asymptotes at f. This rules out e^-x, as it only goes to inf at x=>-inf.
With 1/x hopefully chosen, now we can fix the vertical asymptote by shifting from x-> x-f.
We now have ##\frac{1}{x-f}##, which has a vertical asymptote at f, but horizontal at 0.
Now here is a fork that I'm trying to remedy.
Occam's razor suggests that we should add f, which will fix the horizontal asymptote. It does. So does multiplying by f*x, i.e. ##\frac{fx}{x-f}##. If I follow Occam's razor and plot this function vs. my data, I get a very linear graph with a slope of 2 and y intercept of around -f. This implies that we can add f and multiply by 1/2 to get a good fit. It works, really well, actually. All the data points are within around a centimeter of using the correct fit.
I will attach all 3 graphs with the equations. I added in a bit of random variance to the ##d_i## measurements, so they are all +/- 1cm.
I would really like to end this section by arriving at ##1/f = 1/d_o + 1/d_i##
Any ideas on adjustments that could be made, or why we can/should argue around the "add f" method?
The 3 labeled graphs are as follows:
Correct Fit = ##d_i## vs ##\frac{fd_o}{d_o-f}## which can be arranged into the standard thin lens equation.
Add f = ##d_i## vs ##\frac{1}{d_o-f} + f##
Fix again = ##d_i## vs ##\frac{1}{2}(\frac{1}{d_o-f} + 2f)## , I added f again to fix the intercept, then multiplied by 1/2 to fix the slope.
If need be, I can attach the spreadsheet.
Any ideas or suggestions are appreciated.
What I find really interesting is that the correct fit and fix again trendlines are both very convincing, although correct is objectively ever so slightly better, and over a large data range at that. Horizontal axis is fit values, vertical is simulated data with random variance.
All plots use the same data.