- #1
Aurelius120
- 151
- 16
- TL;DR Summary
- The problem arose when I tried to find the capacitance of two concentric shells when the inner one is earthed. For this it was necessary that the charge on the inner sphere be found. After which they can be treated as parallel combination of capacitors or something similar. However in the absence of an electric field how does charge induce on the inner sphere when a charge is stored on the outer?
So from Gauss theorem, electric field at any point inside a uniformly charged sphereical shell is zero. Thus there is no electrostatic force on the inner sphere.
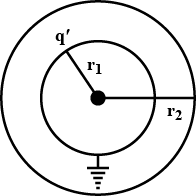
From what I have learnt, a field is necessary to move charges. But in this case the inner sphere acquires a charge q without any force acting on it.
I fully understand the electrostatic potential explanation. That the Earthed sphere must maintain a zero potential therefore some charge flows into it from earth to make net potential zero, according to equation:
$$\frac{Kq}{r_1}+\frac{KQ}{r_2}=0\implies q=\frac{-Qr_1}{r_2}$$
In other cases of electrostatics, movement of charges is explained by field
Why does that fail here? Is field not necessary for motion of charges?
From what I have learnt, a field is necessary to move charges. But in this case the inner sphere acquires a charge q without any force acting on it.
I fully understand the electrostatic potential explanation. That the Earthed sphere must maintain a zero potential therefore some charge flows into it from earth to make net potential zero, according to equation:
$$\frac{Kq}{r_1}+\frac{KQ}{r_2}=0\implies q=\frac{-Qr_1}{r_2}$$
In other cases of electrostatics, movement of charges is explained by field
Why does that fail here? Is field not necessary for motion of charges?
Last edited: