- #1
lost captain
- 6
- 2
- TL;DR Summary
- What's the total pressure ( Patm and Phydrostatic) inside an inverted tube? I am basically referring to that straw experiment we do in physics class when the teacher explains atmospheric pressure.
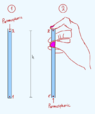
When we learn about atmospheric pressure in physics class, there's this classic experiment with a straw (second drawing). So i wanted to ask about the hydrostatic pressure in that particular experiment.
Is the total pressure at point 1' equal to Patm + ρgh ? So is the total pressure at point 1' essentially the same as the total pressure at pont 1 in the first container? And what about points 2 and 2' do they also have the same pressure?
And just to clarify one more very important thing: when a container filled with water is open to the atmosphere, is the atmospheric pressure distributed throughout the whole container? So, does any point, at any depth, in that container have the same atmospheric pressure?
Is the total pressure at point 1' equal to Patm + ρgh ? So is the total pressure at point 1' essentially the same as the total pressure at pont 1 in the first container? And what about points 2 and 2' do they also have the same pressure?
And just to clarify one more very important thing: when a container filled with water is open to the atmosphere, is the atmospheric pressure distributed throughout the whole container? So, does any point, at any depth, in that container have the same atmospheric pressure?