- #1
Fury22
- 7
- 1
- TL;DR Summary
- Will the lever balance when two equal forces are applied to it?
Hi everyone! I am not a physicist or a physics student. Just a simple video game programmer. I have recently gotten into a discussion with my fellow programmer about a specific hypothetical problem regarding levers. The problem might seem very simple at first, but cause me a bit of headache.
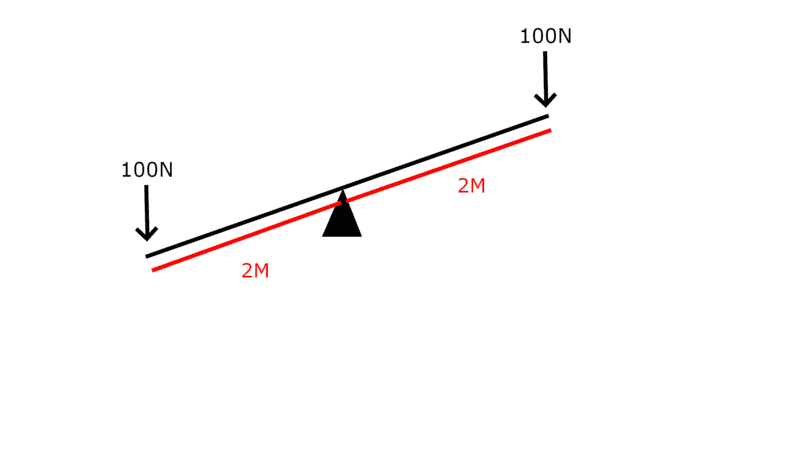
So, let's say we have a lever with support exactly in the middle of it, so both sides arms are exactly the same length.
I apply exactly the same forces at both ends of the lever. Let's say 100 Newtons, or a 100kg objects. The amount of force doesn't matter. What matters is that the arm and the force is exactly the same at both ends.
However the lever initially is tilted all the way to the left side. So we locked the mechanism then placed the weight/force at both ends, and then we release the mechanism.
What happens? Will the lever balance out and rotate, so that it's completely flat? Or will it just stay still the same way when it was released?
If you know the answer, I'd like to know why you think this way.
My opinion:
In my opinion the lever will stay still, because the force on both sides results in equal, but opposite torque. But I might be wrong.
My friend's opinion:
My friend says it will balance itself. If this is true, I am curious what causes a 100kg object on the left to be lifted off the ground by the 100kg object on the right?
Thanks for any answers in advance!
So, let's say we have a lever with support exactly in the middle of it, so both sides arms are exactly the same length.
I apply exactly the same forces at both ends of the lever. Let's say 100 Newtons, or a 100kg objects. The amount of force doesn't matter. What matters is that the arm and the force is exactly the same at both ends.
However the lever initially is tilted all the way to the left side. So we locked the mechanism then placed the weight/force at both ends, and then we release the mechanism.
What happens? Will the lever balance out and rotate, so that it's completely flat? Or will it just stay still the same way when it was released?
If you know the answer, I'd like to know why you think this way.
My opinion:
In my opinion the lever will stay still, because the force on both sides results in equal, but opposite torque. But I might be wrong.
My friend's opinion:
My friend says it will balance itself. If this is true, I am curious what causes a 100kg object on the left to be lifted off the ground by the 100kg object on the right?
Thanks for any answers in advance!
Last edited by a moderator: