- #1
yrob
- 12
- 0
- TL;DR Summary
- What is the force applied on an immobile small sphere by a uniformly flowing fluid with turbulent flow?
Hello everybody,
I am thinking of the following problem:
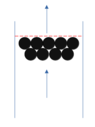
A sphere a radius r is in a much larger container of radius R.
In this container, a fluid continuously flows with turbulent conditions from bottom to top.
I would like to approximate the force pushing the sphere up.
Some calculations I made with F = 0.5 * Cd * rho * A * v**2 (Cd being the drag coefficient that I tried from 0.2 to 0.5, rho the fluid density, A the area of the pipe, and v the fluid vertical velocity) give me incredibly low values, below the gravity force even with enormous flows. Therefore, I believe what I calculated is only the resisting force for the sphere to move in the fluid, and not the force of the fluid on the sphere.
Would you have a hint on that problem?
Thank you.
I am thinking of the following problem:
A sphere a radius r is in a much larger container of radius R.
In this container, a fluid continuously flows with turbulent conditions from bottom to top.
I would like to approximate the force pushing the sphere up.
Some calculations I made with F = 0.5 * Cd * rho * A * v**2 (Cd being the drag coefficient that I tried from 0.2 to 0.5, rho the fluid density, A the area of the pipe, and v the fluid vertical velocity) give me incredibly low values, below the gravity force even with enormous flows. Therefore, I believe what I calculated is only the resisting force for the sphere to move in the fluid, and not the force of the fluid on the sphere.
Would you have a hint on that problem?
Thank you.