Symmetry breaking in the AdS small/large black hole phase transition

I am trying to reproduce the results from this paper where they find out the expression for the Landau functional to be

$$\psi(x,t,p)=\frac{1}{4}(\frac{1}{x}+6x+px^3-4tx^2)$$

We plot the Landau functional v/s the order parameter($x$) at $p=0.5$ and obtain the Figure 4. from the paper as


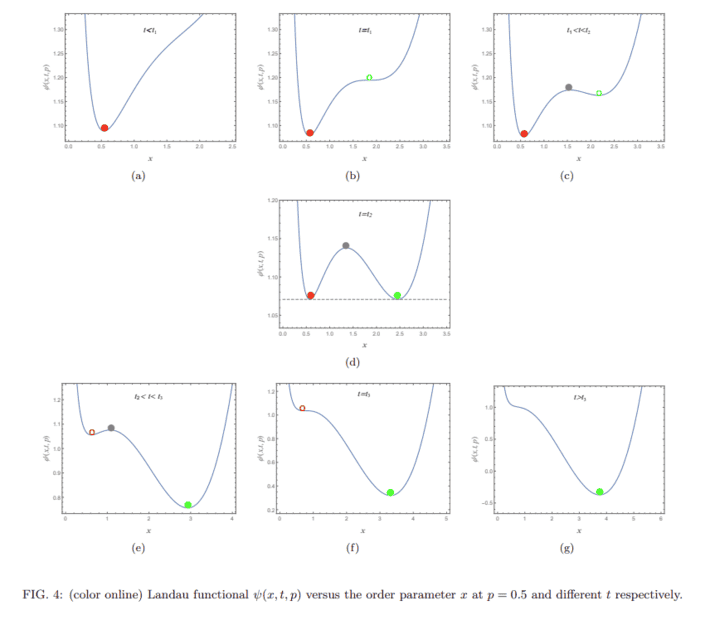
Now according to free energy approach, this is a first-order phase transition. According to Landau theory, every phase transition is related to a symmetry breaking. Which symmetry is being broken here, for this system of AdS black holes?

At least with the van der Waals model, i.e. gas-liquid phase transition, there is no symmetry breaking associated with it. I think it is simply not true that every phase transition is related to a symmetry breaking.

DrDu said:

At least with the van der Waals model, i.e. gas-liquid phase transition, there is no symmetry breaking associated with it. I think it is simply not true that every phase transition is related to a symmetry breaking.

Supposedly Landau theory only fails in that respect in some weird low temperature scenaria, but you are right that I can't really think of how the gas to liquid transition breaks a symmetry... I also can't seem to find it anywhere, maybe someone else knows...

codebpr said:

Which symmetry is being broken here

One can answer this question formally, without understanding physics. Shift the variable ##x## such that the red minimum of the plotted function is at ##x=0##. The minimum ##x=0## is hence invariant under the transformation ##x\to -x##. The green minimum is not invariant under ##x\to -x##, so the broken symmetry is the inversion ##x\to -x##, for the shifted ##x##.

Hm, ok, but this is not a symmetry of the system or its hamiltonian.

DrDu said:

Hm, ok, but this is not a symmetry of the system or its hamiltonian.

True, in general there is no any reason why the Landau functional should have any exact symmetry. But close to the minimum ##x=x_{\rm red}## the functional can be expanded
$$\psi(x,...)=a+b(x-x_{\rm red})^2+...$$
which at least has an approximate symmetry.

EDIT: Or maybe there is always some exact symmetry in the sense of Galois theory?
http://www.cc.kyoto-su.ac.jp/project/MISC/slide/seminar-s/2011/120112Takeuchi.pdf