- #1
greypilgrim
- 506
- 36
Hi.
I've seen single slit diffraction being brought up as an example of the uncertainty principle: Narrowing the slit restricts the particles more in one dimension, which means the momentum in this dimension is more uncertain, which results in a more spread-out diffraction pattern.
I've even seen "derivations" of the uncertainty relation like the following:
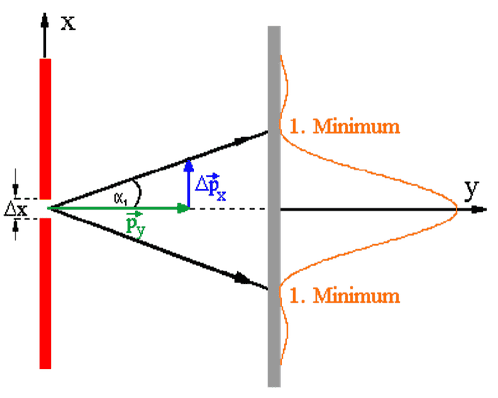
They use the 1st minimum of the pattern to define ##\Delta\vec{p}_x##, and then with ##\sin(\alpha_1)\approx\tan(\alpha_1)## and the de Broglie wavelength successfully arrive at ##\Delta x\cdot\Delta p_x\approx h##.
Well just taking the 1st minimum seems arbitrary. But if I'm not mistaken, a correct derivation of ##\Delta p_x## diverges since ##x^2\sinc^2 (x)## isn't integrable. This of course doesn't contradict the uncertainty principle, but is there a more rigorous way to make sense of it in the case of the single slit?
It's kind of weird that this "spreading out" of the pattern while narrowing the slit isn't reflected in ##\Delta p_x## at all which is always infinite.
I've seen single slit diffraction being brought up as an example of the uncertainty principle: Narrowing the slit restricts the particles more in one dimension, which means the momentum in this dimension is more uncertain, which results in a more spread-out diffraction pattern.
I've even seen "derivations" of the uncertainty relation like the following:
They use the 1st minimum of the pattern to define ##\Delta\vec{p}_x##, and then with ##\sin(\alpha_1)\approx\tan(\alpha_1)## and the de Broglie wavelength successfully arrive at ##\Delta x\cdot\Delta p_x\approx h##.
Well just taking the 1st minimum seems arbitrary. But if I'm not mistaken, a correct derivation of ##\Delta p_x## diverges since ##x^2\sinc^2 (x)## isn't integrable. This of course doesn't contradict the uncertainty principle, but is there a more rigorous way to make sense of it in the case of the single slit?
It's kind of weird that this "spreading out" of the pattern while narrowing the slit isn't reflected in ##\Delta p_x## at all which is always infinite.
Last edited: