Is this a valid quantum Cheshire cat?

I just watched Sabine's Hossenfelder very recent new video on the Quantum Cheshire effect.
From experience, everything Sabine's says on either entanglement/quantum interpretations or not-physics, is heavily biased to her worldview. However I thought it was fun to see what she was going to say about this topic.

She claims that this recent paper : https://iopscience.iop.org/article/10.1088/1367-2630/ad0bd4 finds that the usual interpretation of the quantum Cheshire cat is flawed.

The paper provides a version of the effect using a modified Mach-Zehnder interferometer with a single detector:

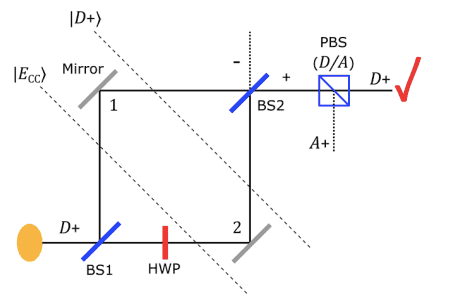
A diagonally polarized light beam (D) is sent from the yellow dot (bottom left), passes by beam splitter BS1 and takes path 1 and path 2. In path 2, there is a half wave polarizer (HWP) rotating the state to an antidiagonally polarized state (A). As the two paths are different they do not recombine when arriving to the second beam splitter BS2. The photons that go to the right, pass by a polarising beamsplitter (PBS), which transmits beams with the original polarization (D) and sends it to the detector (red checkmark in the upper right). If the polarization was rotated
(A), it reflects it away from the detector.

It seems obvious that the photons that took path 1 are able to be detected. Photons that took path 2 seem not to contribute. The Cheshire effect here seems to appear when you slightly modify change the rotation of the HWP by a tiny amount (weak measurement). Under these tiny modifications, it seems that the number of photons detected is modified, implying some kind of quantum Cheshire effect! (modifications of the lower arm should not participate, yet it modifies it, polarization takes a separate path?!).

The result seems trivial, what I cannot understand is what is Cheshire like from it. Clearly modifying anything in the lower arm is going to rotate states in another basis providing more possible photons that can be detected coming from path 2. Sabine makes a similar remark, saying with authority that the interpretation where the cat"disembodied" it finally proven wrong!

The paper seems more conservative, it provides three not equivalent interpretations. I am having a hard time understanding the three different assumptions because they focus too much of contextuality and weak measurement remarks.

What do you think of it? Is this a valid quantum Cheshire cat? It seems too obvious to me, and I hope that I am misunderstanding something (as well as Sabine). It seems very obviously not a quantum effect, where is the catch?

Unless the path of the photon is measured directly by a strong measurement (which in this experiment isn't the case), the statement such as "photon took path 1" is highly interpretation dependent. In most interpretations of QM/QFT, such a statement does not make sense at all.

Demystifier said:

Unless the path of the photon is measured directly by a strong measurement (which in this experiment isn't the case), the statement such as "photon took path 1" is highly interpretation dependent. In most interpretations of QM/QFT, such a statement does not make sense at all.

Sure quantum mechanics has an intrinsically different way of handling it, however if we are going to talk of "Cheshire cats" we have to say what is so no-classical about it.

I would argue that such a systems can be efficiently simulated classically, either with classical waves or with classical pin ball balls: a red pinball ball gets classically stochastically send to either path 1 or 2, in path 2 it changes color to blue, replace the PBS for a ball color selector, if it is red the ball is detected if not the ball gets reflected away. However if there is some slight modification to the color so the ball can sometimes have some red, then it is detected, so now the ball can come from 1 or 2. There is nothing weird about it.

pines-demon said:

I would argue that such a systems can be efficiently simulated classically

I agree. As long as there is no entanglement between two or more parties, quantum phenomena can be simulated classically.

Maybe my comment to an old "experimental" Vaidman paper (I wouldn't have expected to find Vaidman on a paper discussing real experiments) can shed some light on the motivations of those claiming to observe a grin without a cat:

DrChinese said:

*Such as Vaidman 2013 (different paper than above) who also said this, for example: "Quantum mechanics does not provide a clear answer to the question: What was the past of a photon which went through an interferometer ...we conclude that the past of the photons is not represented by continuous trajectories, although a “common sense” analysis adopted in various welcher weg measurements, delayed-choice which-path experiments and counterfactual communication demonstrations yields a single trajectory."

gentzen said:

Looks like this reference is more about the two-state vector formalism and the related theory of weak values than about it being "meaningless to discuss what happens in the quantum world when no one is looking". What is true is that the past of the photons is not represented by continuous trajectories of point particles for the experiments described in the paper. Instead, there is that "two state vector" object with better spatial localization and a better "claim for existence" than the wavefunction (which only exists in the form of probabilies for outcomes of potential measurements). The point of the weak values is that you can look without disturbing things too much, and hence it is meaningful to discuss them even when no one is looking.

Demystifier said:

I agree. As long as there is no entanglement between two or more parties, quantum phenomena can be simulated classically.

There might be some kind of entanglement involved as the spatial trajectory entangles with the polarization state leading to the Bell state

$$\frac{|1\rangle|H\rangle +|2\rangle|V\rangle}{\sqrt2}$$

where ##H## means horizontal and ##V## vertical polarization, 1,2 are the paths.

pines-demon said:

There might be some kind of entanglement involved as the spatial trajectory entangles with the polarization state leading to the Bell state

$$\frac{|1\rangle|H\rangle +|2\rangle|V\rangle}{\sqrt2}$$

where ##H## means horizontal and ##V## vertical polarization, 1,2 are the paths.

You are right, I should have said spatially separated parties. ##|H\rangle## and ##|V\rangle## are not represented by wave functions in position space, so they cannot be thought of as parties at a given position.

1,2 should be something like the momenta of the photons, not positions. There are no position observables for photons!

vanhees71 said:

1,2 should be something like the momenta of the photons, not positions. There are no position observables for photons!

In some cases you can talk of photon position even without the position observable. Take the photon wavefunction in the momentum space, compute its Fourier transform and call it pseudo-wavefunction in the position space. If the pseudo-wavefunction is something like a Gaussian negligible outside of some region R, then for practical purposes it is justified to say that the photon is positioned within R.

Demystifier said:

In some cases you can talk of photon position even without the position observable. Take the photon wavefunction in the momentum space, compute its Fourier transform and call it pseudo-wavefunction in the position space. If the pseudo-wavefunction is something like a Gaussian negligible outside of some region R, then for practical purposes it is justified to say that the photon is positioned within R.

Are you talking about Wigner quasiprobability distribution?

vanhees71 said:

1,2 should be something like the momenta of the photons, not positions. There are no position observables for photons!

I remember that A.Neumaier mentioned that this only applies to 3D positions, not to 2D positions of crossing some 2D surface. In my classical electromagnetic world, I interpret that in the way that there is no position operator corresponding to the 3D energy density, but that doesn't exclude for the scalar product of the Poynting vector with the normal vector of some 2D surface the existence of a corresponding 2D position operator on that surface.

pines-demon said:

Are you talking about Wigner quasiprobability distribution?

No.

When discussing whether something is a quantum Cheshire cat, it might be helpful to have a look at Aharonov's original paper introducing the term and the experimental setup:
https://iopscience.iop.org/article/10.1088/1367-2630/15/11/113015

This is New J. Phys. 15 113015 (2013). It is an open access article.

There, Aharonov also states that the optical implementation of the experiment is not actually that ideal.

Cthugha said:

When discussing whether something is a quantum Cheshire cat, it might be helpful to have a look at Aharonov's original paper introducing the term and the experimental setup:
https://iopscience.iop.org/article/10.1088/1367-2630/15/11/113015

This is New J. Phys. 15 113015 (2013). It is an open access article.

There, Aharonov also states that the optical implementation of the experiment is not actually that ideal.

I was aware of the neutron version not these optical versions.

I was trying to read it but I get lost in the set-up. For example, if I understand correctly Aharonov et al. start with some state, let say ##|\Psi_0\rangle=|H\rangle|R\rangle## where ##H## is horizontal polarization and ##R## means moving to the right. The beam passes by the first beam splitter (BS1) so we get
$$|\Psi\rangle= \frac{(i|L\rangle+|R\rangle)|H\rangle}{\sqrt2} $$
where ##L## means moving to the left and ##i## is just a phase factor from reflection. My problem is what happens next.

Now the beam going to the right crosses a half-wave plate and a phase shifter, is it ok to say that now the state of the system is ##|\Phi\rangle##?:
$$|\Phi\rangle= \frac{|L\rangle|H\rangle+|R\rangle|V\rangle}{\sqrt2} $$
where ##V## means vertical.

And second question, if the above is true. What happens after the second beam splitter (BS2)? What is the state before the detection/PBS?

Note that the figure in the paper seems to suggest that ##|\Phi\rangle## is reached before the HWP and before the BS2.
Edit: if the beam splitter is like the initial one, the state after BS2 seems to be (not sure about the relative phase)
$$|\Phi_2\rangle=\frac{|R\rangle|+\rangle-i|L\rangle|-\rangle}{\sqrt2}$$
where ##|\pm\rangle=(|R\rangle\pm i|L\rangle)/\sqrt2##,in which we only care for the ##|+\rangle## state according to the paper.

Weird enough the paper cited by Sabine seems to invert the postselected state with the preselected state in comparison with Aharonov et al.