- #1
lightlightsup
- 95
- 9
- TL;DR Summary
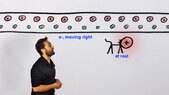
- I understand how relativistic length contraction leads to electrostatic forces on a moving charge next to a current-carrying wire. But, shouldn't this lead to forces on a static charge too?
(1) https://www.youtube.com/results?search_query=relativity+and+electromagnetism
(2)
If I understand this correctly, then, well, shouldn't all current-carrying wires exhibit a small amount of positive charge?
(2)
If I understand this correctly, then, well, shouldn't all current-carrying wires exhibit a small amount of positive charge?