- #1
ohwilleke
Gold Member
- 2,347
- 1,340
- TL;DR Summary
- A new paper with corresponding author is Giorgio Immirzi, the person after whom the somewhat mysterious Immirzi parameter of Loop Quantum Gravity is named claims to explain DM with GR.
A new group of investigators are attempting something similar to Deur's work, which seeks to explain dark matter phenomena with general relativity corrections to Newtonian gravity is systems like galaxies. Deur's most similar publication to this one along these lines was:
I will be reviewing the paper more carefully later, but quickly reviewing the citations, I was struck by the over reliance on Ludwig whose effort to explain dark matter phenomena with GR using the gravito-magnetic effect was quickly debunked as too weak, and by the somewhat disappointing as is the lack of citation of Deur who has published multiple papers on exactly this topic since publishing:
The paper and its abstract are as follows:
Given the five co-authors of the paper including high profile Giorgio Immirzi, this could be the paper that finally gains traction for the argument that the Newtonian approximation of gravity used predominantly in galaxy and galaxy cluster scale astrophysics is materially flawed and that these flaws account for much or all of the phenomena attributed to dark matter, even though the argument has been made in many articles by lower profile authors over the last fifteen years or so.
Notably, this paper stands by the dust model of baryonic matter in galaxies that was seriously questioned when previously advanced by Ludwig.
One thing that makes this new paper notable is that the corresponding author is Giorgio Immirzi, the person after whom the somewhat mysterious Immirzi parameter of Loop Quantum Gravity is named.Alexandre Deur, "Relativistic corrections to the rotation curves of disk galaxies" (April 10, 2020) (lated updated February 8, 2021 in version accepted for publication in Eur. Phys. Jour. C).
I will be reviewing the paper more carefully later, but quickly reviewing the citations, I was struck by the over reliance on Ludwig whose effort to explain dark matter phenomena with GR using the gravito-magnetic effect was quickly debunked as too weak, and by the somewhat disappointing as is the lack of citation of Deur who has published multiple papers on exactly this topic since publishing:
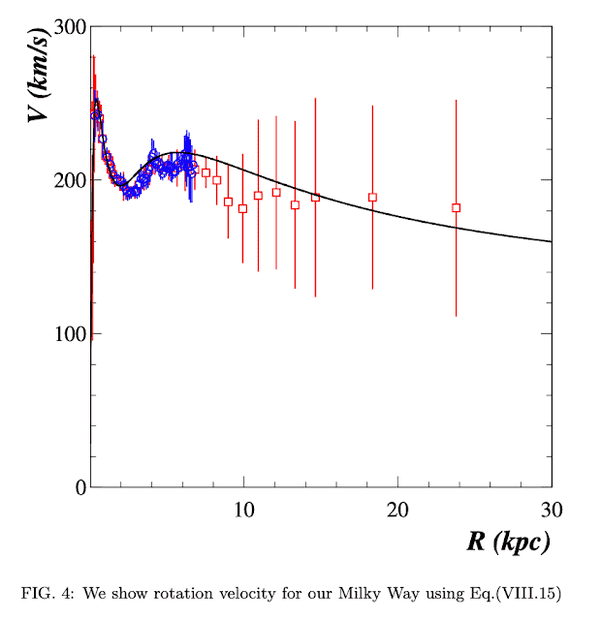
Still, the new paper did produce the following graph which is consistent with the Milky Way galaxy rotation curve without using dark matter or modified gravity, which is worthwhile in and of itself, regardless of who is cited and who gets credit.A. Deur, “Implications of Graviton-Graviton Interaction to Dark Matter” (May 6, 2009) (published at 676 Phys. Lett. B 21 (2009)).
The paper and its abstract are as follows:
A very general class of axially-symmetric metrics in general relativity (GR) that includes rotations is used to discuss the dynamics of rotationally-supported galaxies. The exact vacuum solutions of the Einstein equations for this extended Weyl class of metrics allow us to deduce rigorously the following: (i) GR rotational velocity always exceeds the Newtonian velocity (thanks to Lenz's law in GR); (ii) A non-vanishing intrinsic angular momentum (J) for a galaxy demands the asymptotic constancy of the Weyl (vectorial) length parameter (a) -a behavior identical to that found for the Kerr metric; (iii) Asymptotic constancy of the same parameter also demands a plateau in the rotational velocity.
Unlike the Kerr metric, the extended Weyl metric can and has been continued within the galaxy and it has been shown under what conditions Gauß & Ampére laws emerge along with Ludwig's extended GEM theory with its attendant non-linear rate equations for the velocity field.
Yogendra Srivastava, Giorgio Immirzi, John Swain, Orland Panella, Simone Pacetti, "General Relativity versus Dark Matter for rotating galaxies" arXiv:2207.04279 (July 9, 2022).Better estimates (than that from the Newtonian theory) for the escape velocity of the Sun and a reasonable rotation curve for our own galaxy has been presented.
Given the five co-authors of the paper including high profile Giorgio Immirzi, this could be the paper that finally gains traction for the argument that the Newtonian approximation of gravity used predominantly in galaxy and galaxy cluster scale astrophysics is materially flawed and that these flaws account for much or all of the phenomena attributed to dark matter, even though the argument has been made in many articles by lower profile authors over the last fifteen years or so.
Notably, this paper stands by the dust model of baryonic matter in galaxies that was seriously questioned when previously advanced by Ludwig.
Last edited: