How to Better Define Information in Physics - Comments

Greg Bernhardt submitted a new PF Insights post

How to Better Define Information in Physics


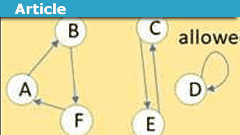
Continue reading the Original PF Insights Post.

Nice essay. Another Insight article that made it on my list of standard references.

Wonderful article @anorlunda, a must read!

Very accessible and very helpful - this is one I will come back to multiple times, @anorlunda .

Greg,
Thanks for this article, very useful in clarifying the term information and yes, there is a great deal of ambiguity in its usage. I come at it along a slightly different path but find myself appreciating your exacting definition.

I also find it useful to distinguish between the two broad species of information – the domestic and the feral -- the former being the abstraction of physical world distinctions by autonomous systems (like me) for purposes of navigation in its broadest sense and the latter, the feral, as the actual physical distinctions found in the repertoire of the physical world. I hope that makes sense.

I have taken it one step further by elevating information to the role of active player in physical dynamic. Distinctions are not simply notables, they must be declared, made manifest and that is the dynamic role of information. I think it is useful and ultimately more accurate to consider information as the constant, active counterpoise to energy. There is never one without the other.

Be interested in your take on that.

Regards,

A very interesting topic that can certainly be twisted around from different perspectives! Indeed, i think it is a very general problem in foundational physics to find objective observerindependent measures. And information measurems or probabilitiy measures are certainly at the heart of this. I will refrain from commenting too much as is risks beeing too biased by my own understanding.

You seem to circle around a desire to formulate a conservation law in terms of principle of least action? Then note that we have the Kullback-Leibler divergence (relative entropy, [itex]S_{K-L}[/itex]) wose minimum can be shown to coincide to maximum transition probability. A possible principle is then to minimize information divergence. The statistical weight in case of a simple dice throwing case puts this into a integration weight of [itex]e^{-MS_{K-L}}[/itex]. You find this relation from basic consideration if you consider the probability of dice-sequences. The factor M is then relted to sample sizes. So we get here both measures of "information" and "amount of data" in the formula.

But when you try to apply this to physics, one soon realizes that the entire construct(computation) is necessary context or observer dependent. This is why relations between observers, becomes complex. Ultimately i think it boils down to the issue of how to attache probability to observational reality of different observers.

So i think this is an important question, but i think one should not expect a simple universal answer. Two observers will generally not in a simple static way agree of information measurems or probability measures. Instead, their disagreement might be interpreted as the basis for interactions.

Edit: If you like me has been thinking in this direction, note the intriguing structural analogies to inertia. Sample size seem to take the place to mass or energy, and information divergence that of inverse temperature. Then ponder what happens when you enlarge the state space with rate of change, or even the conjugate variables. Then the simple dissipative dynamics turns into something non-trivial - but still governed by the same logic.

/Fredrik

I appreciated Gregory Bateson’s characterization of information as the, "difference that makes a difference." I believe he was talking substantively, that “make” was an active verb.

Perhaps it leads to one of those philosophical games of golf without the holes, but may we agree that we dwell in an actual physical world whose dynamic structure is created by its enduring, manifested distinctions.

Corn on one side, cows on the other or a Ph gradient within a cell – these distinctions are made to happen and evolve in time. Information is more than the result of our measurement. In the wild it has an amperage and mediates thermodynamic potential.

This is the way I have come to view it and if the text is flat-footedly declarative it is simply a rhetorical stance seeking comment.

Nice article!

One comment on Noether's Theorem. With regard to energy conservation, Noether's Theorem says that energy conservation is due to time translation symmetry (not reversal). The only role I could see for Noether's Theorem with regard to information conservation would be if there were some well-defined relationship between energy and information, so that if the former were conserved, the latter would also have to be conserved. I can think of some hand-waving arguments that might make that plausible, but I don't know if a rigorous argument along these lines has been formulated.

Btw, since you mentioned Professor Lewin in the article: I had the privilege of taking basic EM physics from him when I was at MIT. The lectures were in a huge lecture hall that seated several hundred, with a stage at the front. When we got there for the first lecture, a fair portion of the stage was occupied by a Van de Graaff generator. It sat there for most of the hour; then, at the very end of the lecture, Lewin said he was going to give a simple demonstration of electrostatics: he fired up the generator, climbed onto a chair, touched a rod to the generator, and then touched the rod to his hair (which was still pretty long back then), which immediately stood on end in all directions.

“Knowledge and Entropy are properties of the system and the state of the system (and possibly external factors too). Information is a property of the system and independent of the state.[iv]”

Reference https://www.physicsforums.com/insights/how-to-better-define-information-in-physics/

Definitions are somewhat a matter of taste. It seems strange to define "information" to be distinct from "knowledge". Your general idea is that "information" has to do with the set of possible states of a type of phenomena (e.g. containers of gas) and that "knowledge" has to do with knowing about subsets of states that are actually possible for a particular example of that phenomena (e.g. facts about a particular container of gas or a particular proper subset of possible containers of gas).

By that approach, defining the "information" of a "system" requires defining its states. However we can define the "states" of phenomena in various ways, and the "information" of a system is only defined after "states" are defined.

For example, a system might obey a not 1-to-1 dynamics given by:
a1 -> b1 or b2
a2 -> b1
b1 -> a1
b2 -> a2
for states a1,a2,b1,b2

A person might choose to define (or only be aware of) a set of two states given by
A = {a1,a2}
B = {b1,b2}
and the 1-to-1dynamics in terms of those states is given by
A->B
B->A

So it seems that questions about preserving information depend on someone's knowledge or discretion in defining the states of a system - in the common language sense of the word "knowledge".

Even better, Liouville’s Theorem[viii] says that if we choose a region in phase space (see D above); it evolves in time to different positions and shapes, but it conserves the volume in phase hyperspace.

My understanding of Liouvilles Theorem is that it deals with a conserved "density" defined on phase space, not with the concept of "volume" alone. Perhaps "phase space" in physics has definition that involves this density in addition to the ordinary mathematical concept of "volume"?