Falling into a massive black hole is not necessarily noticeable

I find it interesting that the more massive the black hole, the weaker the fall acceleration at the distance of the Schwarzschild radius - that's why you wouldn't necessarily notice anything special in the event horizon.

And why do you find that in any way strange?

Kekkuli said:

the fall acceleration at the distance of the Schwarzschild radius

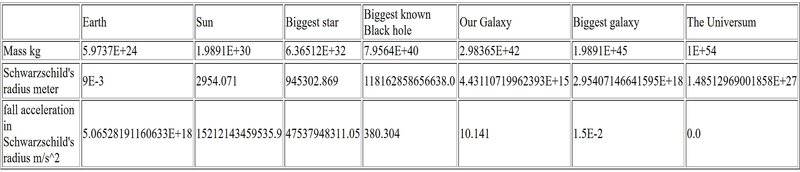
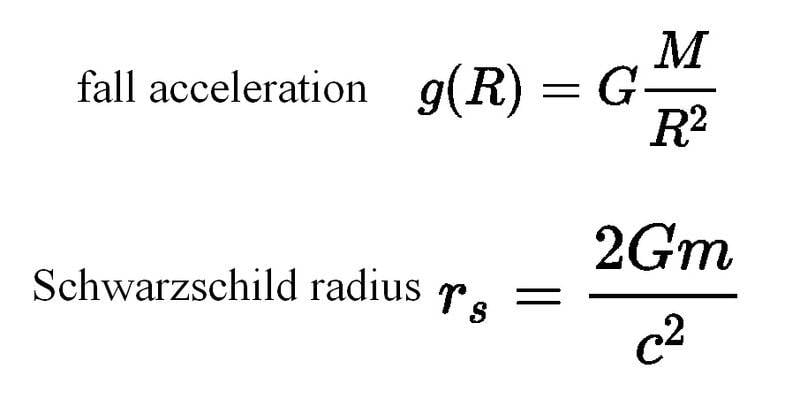
##GM / R^2## is not "the fall acceleration" except in a very technical sense: it is the "redshifted" proper acceleration of an observer "hovering" at ##R##. So, for example, if an observer at infinity were holding up an object at ##R## using a very long rope, ##GM / R^2## is the force per unit mass that the observer at infinity would have to exert on the rope. But the object at ##R## would not experience that acceleration; the object's proper acceleration would be ##GM / (R^2 \sqrt{1 - 2GM / (c^2 R)})##.

(Similar remarks apply to the coordinate acceleration of a free-falling object relative to a hovering observer at ##R##, which I suspect is what you are thinking of as "fall acceleration".)

Also, at the Schwarzschild radius, there are no "hovering" observers; it is impossible to "hover" at the Schwarzschild radius, or for an object to be held there by a very long rope, even for an instant. So even the technical sense of "fall acceleration" above is no longer meaningful at the Schwarzschild radius.

Kekkuli said:

that's why you wouldn't necessarily notice anything special in the event horizon

No, it isn't. You wouldn't notice anything special falling through the horizon because spacetime is locally Lorentzian there just like it is everywhere else. It has nothing to do with "fall acceleration".

I would argue that acceleration is much less relevant than tidal forces. And big BH's have small tides.

Kekkuli said:

I find it interesting that the more massive the black hole, the weaker the fall acceleration at the distance of the Schwarzschild radius - that's why you wouldn't necessarily notice anything special in the event horizon.

Saying "notice" you seem to think of tidal force or spaghettification. Yes, the larger the black hole the less you feel it, as already said in #4. The reason is tidal force goes with 1/M².