- #1
syfry
- 172
- 17
- TL;DR Summary
- I know after inflation (from Planck scale to grapefruit size) the universe expanded at a constant rate, cooling as it did so at various stages of density.
Seeking a comparison to understand the density at each stage which had prevented light from traveling far.
Here's as far as I've gotten in the research (please correct any errors I'm making). The stages of high density had included these periods:
• light at high energy was in a cycle of forming into matter, forming back into light, and so on
• until things cooled enough for nucleons to form
• until things cooled enough for electrons to bind
From what I've had explained, during the 380,000 years (maybe near its end?), the light could actually travel perhaps half a light year to a few light years, before it'd get reabsorbed... so there was probably some empty -ish space, but, the universe was still opaque.
If that's the case, what doesn't make sense is how that emptier part wouldn't be cool enough for electrons to bind. Is it because the emitted light would blast away / unbind electrons that did bond?
But the other part that still isn't intuitive, is how did expansion take hundreds of thousands of years for light to travel freely? I'm thinking that enough expansion would create enough space for nucleons and electrons to form atoms, and for light to travel without bumping into stuff.
How dense was the universe at each stage of density? What can we compare each to?
Was the universe like a neutron star of density in the first few minutes?
When it was midway to becoming transparent to light, was the universe density like our sun? (sort of like how light can take thousands of years to travel from the sun's core to the sun's surface)
When the 380,000 years were almost up, was the universe like a thinner version of a nebula, with open spots of space but still enough bunches of matter to reabsorb light?
And how did it take so long for expansion to spread out the matter? Is it because gravity between particles slowly countered the effect?
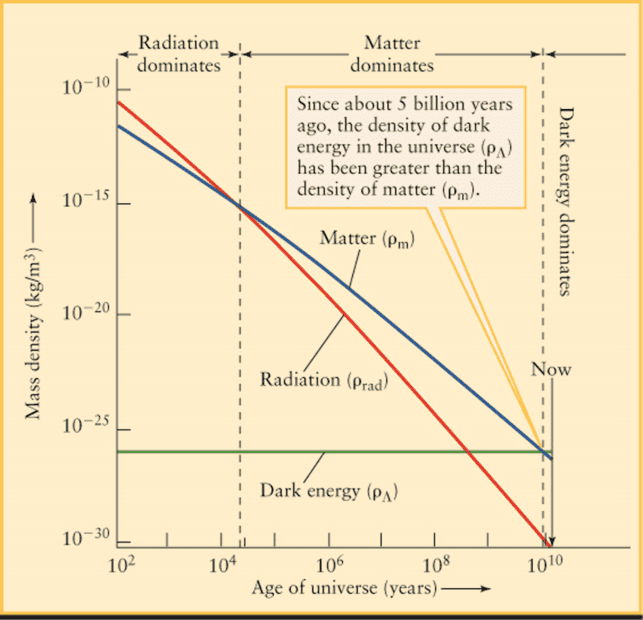
For reference on the rate of expansion, the graph below shows that the rate of expansion has remained exactly steady and consistent:
https://sites.ualberta.ca/~pogosyan/teaching/ASTRO_122/lect30a/6592_fig26_20 [Converted].jpg
• light at high energy was in a cycle of forming into matter, forming back into light, and so on
• until things cooled enough for nucleons to form
• until things cooled enough for electrons to bind
From what I've had explained, during the 380,000 years (maybe near its end?), the light could actually travel perhaps half a light year to a few light years, before it'd get reabsorbed... so there was probably some empty -ish space, but, the universe was still opaque.
If that's the case, what doesn't make sense is how that emptier part wouldn't be cool enough for electrons to bind. Is it because the emitted light would blast away / unbind electrons that did bond?
But the other part that still isn't intuitive, is how did expansion take hundreds of thousands of years for light to travel freely? I'm thinking that enough expansion would create enough space for nucleons and electrons to form atoms, and for light to travel without bumping into stuff.
How dense was the universe at each stage of density? What can we compare each to?
Was the universe like a neutron star of density in the first few minutes?
When it was midway to becoming transparent to light, was the universe density like our sun? (sort of like how light can take thousands of years to travel from the sun's core to the sun's surface)
When the 380,000 years were almost up, was the universe like a thinner version of a nebula, with open spots of space but still enough bunches of matter to reabsorb light?
And how did it take so long for expansion to spread out the matter? Is it because gravity between particles slowly countered the effect?
For reference on the rate of expansion, the graph below shows that the rate of expansion has remained exactly steady and consistent:
https://sites.ualberta.ca/~pogosyan/teaching/ASTRO_122/lect30a/6592_fig26_20 [Converted].jpg
Last edited by a moderator: