Solve the homogenous Neumann problem

• Sep 19, 2022

• #1

chwala

Gold Member

2,573

343

TL;DR Summary

See attached

I am going through this notes and i would like some clarity on the highlighted part...the earlier steps are pretty easy to follow...

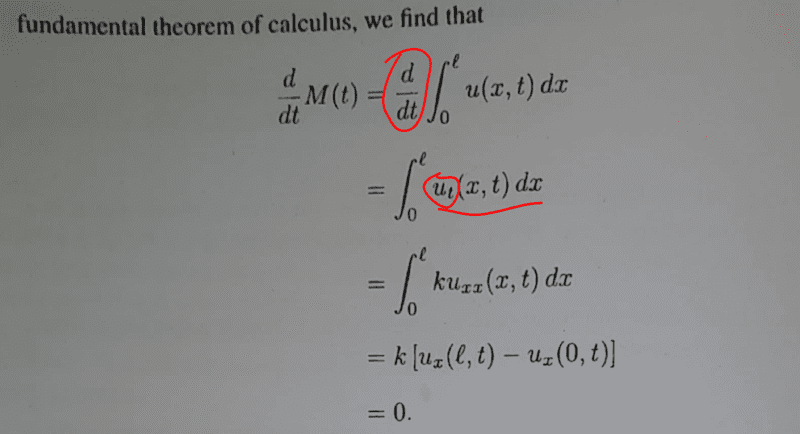
Is there a mistake here...did the author mean taking partial derivative with respect to ##t##? is ##\dfrac{d}{dt}## a mistake? How did that change to next line ##\dfrac{∂}{∂t}##... unless i am the one missing something here. Cheers guys.

 

Last edited: Sep 19, 2022

Physics news on Phys.org

• Research suggests how turbulence can be used to generate patterns
• High-quality microwave signals generated from tiny photonic chip
• Quantum talk with magnetic disks

• Sep 19, 2022

• #2

jedishrfu

Mentor

Insights Author

14,740

9,085

Its just a notation convention, taking the partial is the same as taking a derivative.

As you move the derivative operation inside the integral, you realize that you now have more than one variable and so switch to the partial derivative notation and that you are not taking the derivative of x ie x is independent of t.

 

• Sep 19, 2022

• #3

chwala

Gold Member

2,573

343

jedishrfu said:

Its just a notation convention, taking the partial is the same as taking a derivative.

As you move the derivative operation inside the integral, you realize that you now have more than one variable and so switch to the partial derivative notation and that you are not taking the derivative of x ie x is independent of t.

Thanks for that...considering it as a 'notation convention' makes sense. I was lingering there for some time trying to figure out on what's happening man... thanks @jedishrfu. Bingo!

 

• Sep 19, 2022

• #4

pasmith

Science Advisor

Homework Helper

3,029

1,597

chwala said:

Is there a mistake here...did the author mean taking partial derivative with respect to ##t##? is ##\dfrac{d}{dt}## a mistake? How did that change to next line ##\dfrac{∂}{∂t}##... unless i am the one missing something here. Cheers guys.

[itex]\int_0^l u(x,t)\,dx[/itex] is a function only of [itex]t[/itex], in the same way that [itex]\int_a^b f(x)\,dx[/itex] is just a number: the result of a definite integration is not a function of the dummy variable. So the total derivative is correct. When we swap the order of integation with respect to [itex]x[/itex] and differentiation with respect to [itex]t[/itex] we have by the definitions of total and partial differentiation that [tex]
\begin{split}
\frac{d}{dt}\int_0^l u(x,t)\,dt &=
\lim_{h \to 0} \frac{1}{h}\left(\int_0^l u(x,t+h)\,dx - \int_0^l u(x,t)\,dx\right) \\
&= \int_0^l \lim_{h \to 0} \frac{u(x,t+h) - u(x,t)}{h}\,dx \\
&= \int_0^l u_t(x,t)\,dt.\end{split}[/tex]

 

1. What is the homogenous Neumann problem?

The homogenous Neumann problem is a mathematical problem that involves finding a solution to a partial differential equation with a specific type of boundary condition. In this problem, the boundary condition is that the derivative of the solution at the boundary is equal to zero.

2. Why is solving the homogenous Neumann problem important?

Solving the homogenous Neumann problem is important because it has many applications in physics, engineering, and other fields. It is used to model various physical phenomena, such as heat transfer, diffusion, and wave propagation.

3. What methods are used to solve the homogenous Neumann problem?

There are several methods that can be used to solve the homogenous Neumann problem, including separation of variables, Fourier series, and Green's functions. The choice of method depends on the specific problem and the complexity of the equation.

4. Are there any limitations to solving the homogenous Neumann problem?

Yes, there are some limitations to solving the homogenous Neumann problem. One limitation is that it can only be applied to linear partial differential equations. Additionally, the boundary conditions must be well-defined and the problem must have a unique solution.

5. How is the homogenous Neumann problem related to other boundary value problems?

The homogenous Neumann problem is closely related to other boundary value problems, such as the Dirichlet and Robin problems. These problems differ in the type of boundary condition that is imposed, but they all involve finding a solution to a partial differential equation subject to certain boundary conditions.