Outer measure .... Axler, Result 2.8 ....

I am reading Sheldon Axler's book: Measure, Integration & Real Analysis ... and I am focused on Chapter 2: Measures ...

I need help with the proof of Result 2.8 ...

Result 2.8 and its proof read as follows


In the above text from Axler we read:"The doubly indexed collection of open intervals \(\displaystyle \{ I_{ j, k } : j,k \in \mathbb{Z^+} \} \) can be rearranged into a sequence of open intervals whose union contains \(\displaystyle \bigcup_{ k = 1 }^{ \infty} A_k \) as follows, where in step k (start with k =2, then k = 3,4,5 ... ) we adjoin the k-1 intervals whose indices add up to k :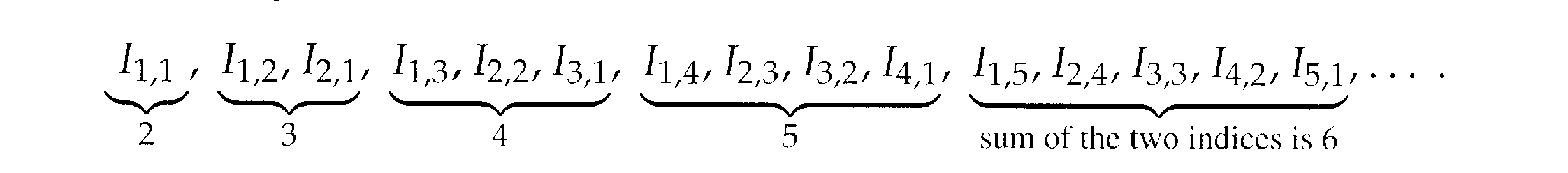Inequality 2.9 shows that the sum of the lengths listed above is less than or equal to \(\displaystyle \epsilon + \sum_{k=1}^{ \infty} |A_k| \). Thus \(\displaystyle | \sum_{k=1}^{ \infty} A_k | \leq \epsilon + \sum_{k=1}^{ \infty} |A_k| \) ... ..."

i really do not understand what is going on here ... can someone explain why we are arranging or grouping the intervals \(\displaystyle \{ I_{ j, k } : j,k \in \mathbb{Z^+} \} \) in this way and why exactly it follows that the sum of the lengths listed above is less than or equal to $ \epsilon + \sum_{k=1}^{ \infty} |A_k| $ ...Hope someone can help,

Peter
NOTE: so that readers of the above post will have enough contextual and notational information i am posting the start of Axler's Section @A on Outer Measure ... as follows:


Hope that helps Peter

Hi Peter,

The reason the author is doing things this way is because the outer measure is defined as an infimum. Recall that the infimum of a set of real numbers is the greatest lower bound of that set of real numbers.

According to Definition 2.2, if for an arbitrarily fixed $\varepsilon >0$ there is a collection of open intervals whose union contains $\displaystyle\bigcup_{k=1}^{\infty}A_{k}$ and the sum of whose lengths is less than or equal to $\varepsilon + \displaystyle\sum_{k=1}^{\infty}|A_{k}|$, then (by definition of infimum) $\left|\displaystyle\bigcup_{k=1}^{\infty}A_{k}\right|\leq \varepsilon + \displaystyle\sum_{k=1}^{\infty}|A_{k}|$. Since $\varepsilon > 0$ is arbitrary, it then follows that $ \left|\displaystyle\bigcup_{k=1}^{\infty}A_{k}\right|\leq \displaystyle\sum_{k=1}^{\infty}|A_{k}|$. This is the line of reasoning the author is following.

To establish that the union of the open intervals $I_{j,k}$ contains $\displaystyle\bigcup_{k=1}^{\infty}A_{k}$, the author is using an adapted version of Cantor's diagonal argument proving the countability of the rational numbers, where
$$I_{1,1}\quad I_{1,2} \quad I_{1,3},\,\ldots\\
I_{2,1}\quad I_{2,2}\quad I_{2,3},\,\ldots\\
\vdots$$
replaces the fractions seen in the link to Cantor's argument shared above. Since the open intervals in row $k$ are chosen specifically to cover $A_{k}$, as the author snakes their way through the sets via Cantor's diagonal argument, we can be sure the union of all $A_{k}$'s is covered, too.

According to the way the open intervals in row $k$ were chosen, we know that the sum of the lengths of the open intervals in row $k$ is bounded above by $\dfrac{\varepsilon}{2^{k}} + |A_{k}|$; i.e., $$\displaystyle\sum_{j=1}^{\infty}\mathcal{l}(I_{j,k})\leq \dfrac{\varepsilon}{2^{k}} + |A_{k}|$$
Since the above is true for all $k$, we can sum the above over $k$ and use the fact that $\displaystyle\sum_{k=1}^{\infty}\dfrac{1}{2^{k}} = 1$ (see Geometric Series - Wikipedia) to obtain
$$\sum_{k=1}^{\infty}\sum_{j=1}^{\infty}\mathcal{l}(I_{j,k})\leq \varepsilon + \sum_{k=1}^{\infty}|A_{k}|$$
Hopefully this helps. Feel free to let me know if you have any other questions.

Hi Peter,

I'm also currently studying Axler's book and I can try to explain the proof of Result 2.8 to you.

First, let's define some terms and notation that Axler uses in this section. The set \{ I_{j,k} : j,k \in \mathbb{Z^+} \} is a collection of open intervals, where the indices j and k represent the starting and ending point of each interval. The notation \bigcup_{k=1}^{\infty} A_k means the union of all the sets A_1, A_2, A_3, ... and so on. In step k of the rearrangement process, we are adding k-1 intervals whose indices add up to k. For example, in step 2, we add the intervals I_{1,1} and I_{2,1} since 1+1=2. In step 3, we add the intervals I_{1,2}, I_{2,1} and I_{3,1} since 1+2=3.

Now, let's look at the inequality 2.9. This inequality shows that the sum of the lengths of the intervals in the collection \{ I_{j,k} : j,k \in \mathbb{Z^+} \} is less than or equal to \epsilon + \sum_{k=1}^{\infty} |A_k|. This means that we can make the sum of the lengths of the intervals as close to \sum_{k=1}^{\infty} |A_k| as we want by choosing a small enough \epsilon. This is important because we want to show that the union of all the A_k sets is contained within the union of the open intervals.

Now, let's look at the last part of the proof where we have | \sum_{k=1}^{\infty} A_k | \leq \epsilon + \sum_{k=1}^{\infty} |A_k|. This inequality follows from the previous part of the proof where we showed that the sum of the lengths of the intervals is less than or equal to \epsilon + \sum_{k=1}^{\infty} |A_k|. Since the sum of the lengths is less than or equal to \epsilon + \sum_{k=1}^{\infty