PD code yields two different knot diagrams

• Aug 2, 2022

• #1

sophiatev

39

4

TL;DR Summary

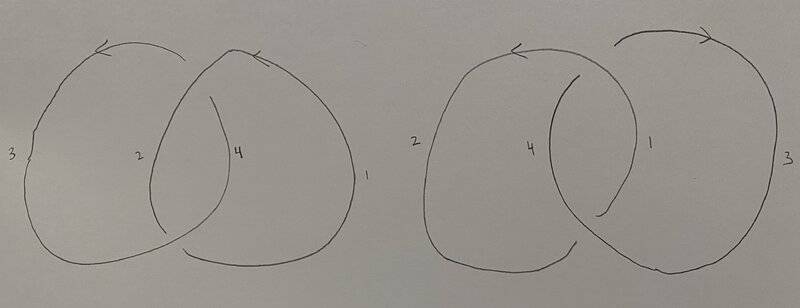
The same PD code seems to yield two different knot diagrams of the Hopf link

The PD code [(2, 3, 1, 4), (4, 1, 3, 2)] seems to map to a non-unique knot diagram. I can describe the following two Hopf links with different orientations with this same PD code. As I understand it, while a link diagram does not have a unique PD code, a given PD code should map to just one knot diagram. Am I missing something?

 

Physics news on Phys.org

• Research suggests how turbulence can be used to generate patterns
• High-quality microwave signals generated from tiny photonic chip
• Quantum talk with magnetic disks

• Aug 2, 2022

• #2

jedishrfu

Mentor

Insights Author

14,740

9,085

Are these supposed to be knots? Both diagrams look like two interconnected rings not knots. Perhaps that's why things aren't working.

Here's a trefoil knot that looks similar to yours but has an extra loop:

https://en.wikipedia.org/wiki/Trefoil_knot

and here's a table of many knots:

http://katlas.org/wiki/The_Rolfsen_Knot_Table

 

• Aug 3, 2022

• #3

sophiatev

39

4

Sorry, the PD code maps to a unique *link* diagram, so the Hopf link is a valid diagram (also, a ring is the unknot so it's still a knot, right? The Hopf link is just two linked unknots)

 

• Aug 3, 2022

• #4

Maarten Havinga

76

41

I don't know if it helps, but:

Make half a turn (the least complicated direction) of one of the 4 rings around the horizontal axis.

 

What is a PD code?

A PD code, also known as a planar diagram code, is a way of representing a knot or link in three-dimensional space using a sequence of symbols and numbers. It is a common notation used in knot theory and is often used to study the properties of knots and links.

How can a PD code yield two different knot diagrams?

A PD code can yield two different knot diagrams when the code is interpreted in different ways. This can happen if the code contains crossings that can be interpreted in two different orientations. In other words, the code can be read from left to right or right to left, resulting in two different knot diagrams.

Why is it important to consider both knot diagrams from a PD code?

Considering both knot diagrams from a PD code is important because it allows us to study the properties of a knot or link from different perspectives. Each diagram may reveal different information about the knot, and studying both can lead to a better understanding of its structure and behavior.

Can a PD code have more than two different knot diagrams?

Yes, a PD code can have more than two different knot diagrams. This can happen if the code contains multiple crossings that can be interpreted in different ways, resulting in more than two possible diagrams. In general, the number of different diagrams from a PD code is equal to the number of crossings in the code.

Are there any applications for studying multiple knot diagrams from a PD code?

Yes, there are several applications for studying multiple knot diagrams from a PD code. One example is in DNA research, where knot diagrams can be used to study the structure and behavior of DNA strands. Additionally, studying multiple knot diagrams can also help in understanding the properties of physical knots used in various fields such as sailing and rock climbing.