How to compute the Casimir element of Lie algebra sl(2)?

Homework Statement: please, could you help me to know hoe I compute the Casimir element of lie algebra sl(2), I know the basis and their relations, but i could not find the book explain in details how we get the Casimir element.. I think it is related to killing form, but also I could not find the final matrix( as you see in attachment).

I would appreciate if you could help

thank in advance,
Relevant Equations: Casimir element is : C= 4FE+H(H+2)

I have attached the file

I'm not sure about the method you're trying to use, but a Casimir operator is symmetric in all generators. So you just have to write the most general symmetric quadratic expression that you construct from the basic generators, and then compute commutators to narrow it down to the Casimir.

(Btw, you should probably make the effort to learn how to use Latex in this forum. Many potential helpers don't like reading handwritten scribbles. The PF Latex guide can be found under the "Help" button, located bottom right on most PF webpages.)

thank you so much, please could you give me a reference or example of the method you talk about.

in the attached fiel, page 28, it is about how we can find it, but i could not get the idea, how we compute the daul basis.

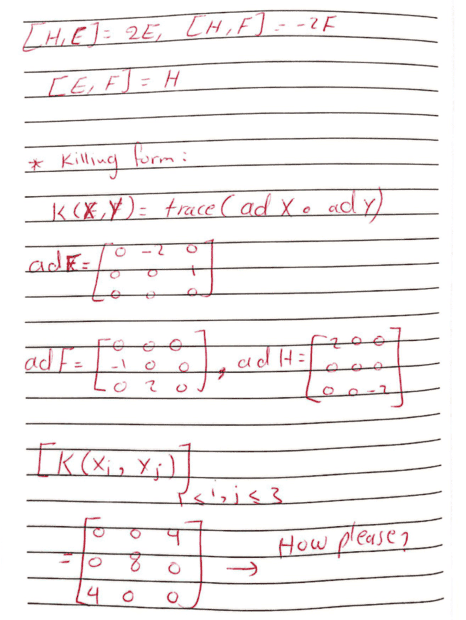
i would apprecite if you could help me to understand it.

Which textbook is that example taken from?

strangerep said:

Which textbook is that example taken from?

hi my Dear, thank you so much for your reply,
the book is :
Introduction to Lie Algebras and Representation Theory
Third Printing, Revised,
J. E. Humphreysthanks in advance,

Why don't you calculate the Killing form?
\begin{align*}
\operatorname{ad}(X)&=x_1\operatorname{ad}(E)+x_2\operatorname{ad}(H)+x_3\operatorname{ad}(F)=
\begin{pmatrix}2x_2&-2x_1&0\\-x_3&0&x_1\\0&2x_3&-2x_2\end{pmatrix}\\[6pt]
\operatorname{ad}(X)\operatorname{ad}(Y)&=\begin{pmatrix}4x_2y_2+2x_1y_3&4x_2y_1&-2x_1y_1 \\ 2x_3y_2&2x_1y_3+2x_3y_1&2x_1y_2\\ -2x_3y_3&4x_2y_3&4x_2y_2+2x_3y_1\end{pmatrix} \\[8pt]
K(X,Y)&=4x_2y_2+2x_1y_3+2x_1y_3+2x_3y_1+4x_2y_2+2x_3y_1\\[6pt]
&=4x_1y_3+8x_2y_2+4x_3y_1
\end{align*}
If we set ##X^{(1)}=E=(1,0,0)\, , \,X^{(2)}=H=(0,1,0)\, , \,X^{(3)}=F=(0,0,1)## then we need to find ##Y^{(1)}\, , \,Y^{(2)}\, , \,Y^{(3)}## such that ##K\left(X^{(i)},Y^{(j)}\right)=\delta_{ij}.## Each ##Y^{(j)}## has coordinates ##Y^{(j)}=(y_1^{(j)},y_2^{(j)},y_3^{(j)})=y_1^{(j)}\cdot E +y_2^{(j)}\cdot H+y_3^{(j)}\cdot F.##

These are ##9## unknowns and ##9## linear equations. Solve it. Then we get
$$
c_{\operatorname{ad}}(K)=\operatorname{ad}(E)\circ \operatorname{ad}(Y^{(1)})+\operatorname{ad}(H)\circ \operatorname{ad}(Y^{(2)})+\operatorname{ad}(F)\circ \operatorname{ad}(Y^{(3)})
$$
with the trace ##\operatorname{trace}(c_{\operatorname{ad}}(K))=K(E,Y^{(1)})+K(H,Y^{(2)})+K(F,Y^{(3)})=3## ...

... if neither you nor I made any mistakes with the signs and indices.

Dear Fresh_42, thank you so much from the bottom of my heart for your help,

please, please, I have a question, here:

If we set $X^{(1)}=E=(1,0,0), X^{(2)}=H=(0,1,0), X^{(3)}=F=(0,0,1)$ then we need to find $Y^{(1)}, Y^{(2)}, Y^{(3)}$ such that $K\left(X^{(i)}, Y^{(j)}\right)=\delta_{i j}$. Each $Y^{(j)}$ has coordinates
$$
Y^{(j)}=\left(y_1^{(j)}, y_2^{(j)}, y_3^{(j)}\right)=y_1^{(j)} \cdot E+y_2^{(j)} \cdot H+y_3^{(j)} \cdot F
$$

how we can solve this, just give the first step, i could not get it,

i need to get this matrix, please bear with me,

$$
\begin{aligned}
& {\left[K\left(x_i, x_j\right)\right]} \\
& =\left[\begin{array}{lll}
0 & 0 & 4 \\
0 & 8 & 0 \\
4 & 0 & 0
\end{array}\right] \rightarrow \text { How please? }
\end{aligned}
$$

thank you so much in advance,

The basis ##(E,H,F)## of ##\mathfrak{sl}(2)## is nice, but if we have to solve nine equations in nine variables it will get a mess with only letters. Therefore we need indices. Say ##X_1=E\, , \,X_2=H\, , \,X_3=F.##

If general vectors are ##X=x_1X_1+x_2X_2+x_3X_3## and ##Y=y_1X_1+y_2X_2+y_3X_3## then we have ##K(X,Y)=4x_1y_3+8x_2y_2+4x_3y_1.##

We have the adjoint representation in this case. We need to find the dual basis for the Casimir element. The Killing-form of the special linear algebra is non-degenerate so a dual basis exists, say it is
$$
\left(Y_1,Y_2,Y_3 \right)=(y_{11}X_1+y_{12}X_2+y_{13}X_3,y_{21}X_1+y_{22}X_2+y_{23}X_3,y_{31}X_1+y_{32}X_2+y_{33}X_3)
$$
expressed in the basis ##(E,H,F).## Then we have to solve
\begin{align*}
1&=K(X_1,Y_1)=K(X_1,y_{11}X_1+y_{12}X_2+y_{13}X_3)=4y_{13}\text{ as } x_1=1,x_2=0,x_3=0\\
0&=K(X_1,Y_2)=K(X_1,y_{21}X_1+y_{22}X_2+y_{23}X_3)=4y_{23}\text{ as } x_1=1,x_2=0,x_3=0\\
0&=K(X_1,Y_3)=K(X_1,y_{31}X_1+y_{32}X_2+y_{33}X_3)=4y_{33}\text{ as } x_1=1,x_2=0,x_3=0\\[6pt]
0&=K(X_2,Y_1)=K(X_2,y_{11}X_1+y_{12}X_2+y_{13}X_3)=8y_{12}\text{ as } x_1=0,x_2=1,x_3=0\\
1&=K(X_2,Y_2)=K(X_2,y_{21}X_1+y_{22}X_2+y_{23}X_3)=8y_{22}\text{ as } x_1=0,x_2=1,x_3=0\\
\ldots&
\end{align*}

This gives us the dual basis ##(Y_1,Y_2,Y_3)## expressed in the basis ##(X_1,X_2,X_3)=(E,H,F).## Seems the result will be
$$
\begin{pmatrix}1/4&0&0\\ 0&1/8&0\\ 0&0&1/4 \end{pmatrix}
$$

That would make sense since
$$
K(X_1,Y_1)+K(X_2,Y_2)+K(X_3,Y_3)=4\cdot 1 \cdot \dfrac{1}{4}+8\cdot 1\cdot \dfrac{1}{8}+4\cdot 1\cdot \dfrac{1}{4}=3
$$

ear Fresh_42,
thank you so much,

I have a question please:$$
\begin{aligned}
& K(X, Y)=4 x_1 y_3+8 x_2 y_2+4 x_3 y_1 \\
& K\left(X_1, Y_1\right)=k\left(X_1, y_{11} X_1+y_{12} X_2+y_{13} X_3\right) \\
& X_1=E, \quad X_2=H, \quad X_3=F \\
& \Rightarrow \quad 1=K\left(E, Y_1\right)=K\left(E, y_{11} E+y_{12} H+y_{13} F\right) \\
& K(x, y)=\operatorname{trace}(\operatorname{ad} X \cdot a d Y_1) \\
& =\operatorname{trace}\left(\operatorname{ad} E \cdot \operatorname{ad}\left(y_{11} E+y_{12} H+y_{13} F\right)\right. \\
&
\end{aligned}
$$

$$
\begin{aligned}
& \operatorname{ad} E=\left(\begin{array}{ccc}
0 & -2 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{array}\right) \\
& y_{11}\left(\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right)+y_{12}\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)+y_{13}\left(\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right) \\
& =\left(\begin{array}{ll}
0 & y_{11} \\
0 & 0
\end{array}\right)+\left(\begin{array}{cc}
y_{12} & 0 \\
0 & -y_{12}
\end{array}\right)+\left(\begin{array}{ll}
0 & 0 \\
y_{13} & 0
\end{array}\right)=\left(\begin{array}{ll}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{array}\right) \\
& \text { How we compute the trace of }\left(\begin{array}{cc}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{array}\right) \\
& \text { let: } Z=\left(\begin{array}{ll}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{array}\right)
\end{aligned}
$$

Is that true, please:

$$
\operatorname{ad}_Z(E)=[Z, E]
$$here please:

$$
1=K\left(X_1, Y_1\right)=K\left(X_1, y_{11} X_1+y_{12} X_2+y_{13} X_3\right)=4 y_{13} \text { as } x_1=1, x_2=0, x_3=0
$$
is it $$y_{13}$$ or $$y_{11}$$
thank you so much,

HDB1 said:

ear Fresh_42,
thank you so much,

I have a question please:$$
\begin{aligned}
& K(X, Y)=4 x_1 y_3+8 x_2 y_2+4 x_3 y_1 \\
& K\left(X_1, Y_1\right)=k\left(X_1, y_{11} X_1+y_{12} X_2+y_{13} X_3\right) \\
& X_1=E, \quad X_2=H, \quad X_3=F \\
& \Rightarrow \quad 1=K\left(E, Y_1\right)=K\left(E, y_{11} E+y_{12} H+y_{13} F\right) \\
& K(x, y)=\operatorname{trace}(\operatorname{ad} X \cdot a d Y_1) \\
& =\operatorname{trace}\left(\operatorname{ad} E \cdot \operatorname{ad}\left(y_{11} E+y_{12} H+y_{13} F\right)\right. \\
&
\end{aligned}
$$

$$
\begin{aligned}
& \operatorname{ad} E=\left(\begin{array}{ccc}
0 & -2 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{array}\right) \\
& y_{11}\left(\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right)+y_{12}\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)+y_{13}\left(\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right) \\
& =\left(\begin{array}{ll}
0 & y_{11} \\
0 & 0
\end{array}\right)+\left(\begin{array}{cc}
y_{12} & 0 \\
0 & -y_{12}
\end{array}\right)+\left(\begin{array}{ll}
0 & 0 \\
y_{13} & 0
\end{array}\right)=\left(\begin{array}{ll}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{array}\right) \\
& \text { How we compute the trace of }\left(\begin{array}{cc}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{array}\right) \\
& \text { let: } Z=\left(\begin{array}{ll}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{array}\right)
\end{aligned}

The trace is the sum of the diagonal elements, hence ##\operatorname{trace}\begin{pmatrix}
y_{12} & y_{11} \\
y_{13} & -y_{12}
\end{pmatrix}=y_{12}+(-y_{12})=0## which was expected for a matrix from ##\mathfrak{sl}(2).##

HDB1 said:

$$

Is that true, please:

$$
\operatorname{ad}_Z(E)=[Z, E]
$$

That is the definition of the adjoint representation, yes. It is the Lie algebra acting on itself by left-multiplication. The Jacobi identity is in that case the condition of a representation.

##\dim \mathfrak{sl}(2)=2^2-1=3## so the matrices of ##\operatorname{ad}(\mathfrak{sl}(2))## are ##3\times 3## matrices.

HDB1 said:

here please:

$$
1=K\left(X_1, Y_1\right)=K\left(X_1, y_{11} X_1+y_{12} X_2+y_{13} X_3\right)=4 y_{13} \text { as } x_1=1, x_2=0, x_3=0
$$
is it $$y_{13}$$ or $$y_{11}$$
thank you so much,

It is
\begin{align*}
K(X_1,Y)&=K(1\cdot X_1+0\cdot X_2+0\cdot X_3\, , \,y_{11} X_1+y_{12} X_2+y_{13} X_3)\\
&=K\left(\begin{pmatrix}x_1\\x_2\\x_3 \end{pmatrix}\, , \,\begin{pmatrix}y_{11},y_{12},y_{13}\end{pmatrix}\right)\\
&=4 \cdot x_1\cdot y_{13}+8\cdot x_2\cdot y_{12}+4\cdot x_3\cdot y_{11}\\
&=4\cdot 1\cdot y_{13}+ 8\cdot 0\cdot y_{12}+4\cdot 0 y_{11}\\
&=4y_{13}
\end{align*}
Therefore ##1=K(X_1,Y)=4y_{13}## since ##X_1=(1,0,0).##

Dear Fresh_42, thank you so much, words cannot express how grateful I am to you,

Here please:
$$
\begin{aligned}
K(X, Y) & =4 x_2 y_2+2 x_1 y_3+2 x_1 y_3+2 x_3 y_1+4 x_2 y_2+2 x_3 y_1 \\
& =4 x_1 y_3+8 x_2 y_2+4 x_3 y_1
\end{aligned}
$$please, how did you commute this, sorry to bother you:

$$
\begin{aligned}
K\left(X_1, Y\right) & =K\left(1 \cdot X_1+0 \cdot X_2+0 \cdot X_3, y_{11} X_1+y_{12} X_2+y_{13} X_3\right) \\
& =K\left(\left(\begin{array}{l}
x_1 \\
x_2 \\
x_3
\end{array}\right),\left(y_{11}, y_{12}, y_{13}\right)\right)
\end{aligned}
$$

finally, the killng form will be this? please:

$$
K(x, y)=\left(\begin{array}{lll}
y_{11} & y_{12} & y_{13} \\
y_{21} & y_{22} & y_{23} \\
y_{31} & y_{32} & y_{33}
\end{array}\right)
$$thanks a lot,

HDB1 said:

Dear Fresh_42, thank you so much, words cannot express how grateful I am to you,

Here please:
$$
\begin{aligned}
K(X, Y) & =4 x_2 y_2+2 x_1 y_3+2 x_1 y_3+2 x_3 y_1+4 x_2 y_2+2 x_3 y_1 \\
& =4 x_1 y_3+8 x_2 y_2+4 x_3 y_1
\end{aligned}
$$

I computed this from your matrices for ##\operatorname{ad}E, \operatorname{ad}H, \operatorname{ad}F.##
An arbitrary vector looks like ##X=x_1E+x_2H+x_3F## and ##Y## accordingly. ##\operatorname{ad}## is linear, so ##\operatorname{ad}X=x_1\operatorname{ad}E+x_2\operatorname{ad}H+x_3\operatorname{ad}F ## and the same with ##\operatorname{ad}Y.##

You already had calculated all matrices ##\operatorname{ad}E, \operatorname{ad}H, \operatorname{ad}F## so I had only to construct ##\operatorname{ad}X## and ##\operatorname{ad}Y.## Then I multiplied them with https://www.symbolab.com/solver/matrix-calculator (sorry for laziness) and since
$$
K(X,Y)=\operatorname{trace}(\operatorname{ad}X \cdot \operatorname{ad}Y)
$$
I finally added all entries on the main diagonal which was ##K(X,Y)=4x_1y_3+8x_2y_2+4x_3y_1\quad (*).##

(You had the same result but on the wrong diagonal. You probably switched indices somewhere.)

HDB1 said:

please, how did you commute this, sorry to bother you:

$$
\begin{aligned}
K\left(X_1, Y\right) & =K\left(1 \cdot X_1+0 \cdot X_2+0 \cdot X_3, y_{11} X_1+y_{12} X_2+y_{13} X_3\right) \\
& =K\left(\left(\begin{array}{l}
x_1 \\
x_2 \\
x_3
\end{array}\right),\left(y_{11}, y_{12}, y_{13}\right)\right)
\end{aligned}
$$

I did this with the formula above. But we have to find (setting ##X_1=E, X_2=H,X_3=F##) three vectors ##Y_1,Y_2,Y_3## such that ##K(X_i,Y_j)=\delta_{ij}\quad (**).##

So I wrote ##Y_j=y_{j1}X_1+y_{j2}X_2+y_{j3}X_3## for ##j=1,2,3.## The ##X_i## are ##X_1=1\cdot X_1+0\cdot X_2+0\cdot X_3## and so on. Now I fed the formula ##(*)## with these coordinates and solved ##(**).##

HDB1 said:

finally, the killng form will be this? please:

$$
K(x, y)=\left(\begin{array}{lll}
y_{11} & y_{12} & y_{13} \\
y_{21} & y_{22} & y_{23} \\
y_{31} & y_{32} & y_{33}
\end{array}\right)
$$thanks a lot,

No. The Killing form is a number, a trace, the sum of diagonal entries of a matrix which is a product of two matrices. In our example we have ...

##\operatorname{ad}## is a linear function from the three-dimensional vector space ##\mathfrak{sl}(2)=\operatorname{lin\,span}\{X_1=E,X_2=H,X_3=F\}## into the nine-dimensional vector spcace of ##3\times 3## matrices ##\mathfrak{gl}(\mathfrak{sl}(2)).##

That ##E,H,F## are themselves two-dimensional matrices is no longer of interest. ##\operatorname{ad}E,\operatorname{ad}H,\operatorname{ad}F## are three-dimensional matrices with ##9=3^2## entries. Say ##\operatorname{ad}(X)=(x_{ij})## and ##\operatorname{ad}Y=(y_{kl})## where all indices run from ##1## to ##3##, then
\begin{align*}
\operatorname{ad}(X) \cdot \operatorname{ad}(Y)&=\left(\sum_{j=1}^3 x_{pj}y_{jq}\right)_{pq}\\[6pt]
\operatorname{trace}\left(\operatorname{ad}(X) \cdot \operatorname{ad}(Y)\right)&=
K(X,Y)=\sum_{k=1}^3 \left(\sum_{j=1}^3 x_{kj}y_{jk}\right)_{kk}
\end{align*}
This is how I calculated the Killing form above, starting with the matrices for ##\operatorname{ad}E,\operatorname{ad}H,\operatorname{ad}F,## then using the matrix calculator for the multiplication ##\operatorname{ad}X\cdot \operatorname{ad}Y## and finally adding all the entries on the main diagonal.

So all in all we have:
\begin{align*}
\mathfrak{sl}(2) &\stackrel{\operatorname{ad}}{\longrightarrow } \mathfrak{gl}(3)\\[6pt]
X &\longmapsto (Y \longmapsto \operatorname{ad}X(Y)= [X,Y])
\end{align*}

___________________
Just a last remark that might confuse you, so don't panic. The adjoint representation is a Lie algebra homomorphism. So its kernel is an ideal in ##\mathfrak{sl}(2).## But ##\mathfrak{sl}(2)## is simple and has no ideals. Hence the kernel is either ##\{0\}## or the entire Lie algebra ##\mathfrak{sl}(2).## The latter would imply that ##\operatorname{ad}=0## which it is not. Thus the kernel is zero and ##\operatorname{ad}## injective. Hence the image ##\operatorname{ad}(\mathfrak{sl}(2)) ## is a three-dimensional simple Lie algebra in the nine-dimensional Lie algebra ##\mathfrak{gl}(\mathfrak{sl}(2))=\mathfrak{gl}(3)## that is isomorphic to
\begin{align*}
\mathfrak{sl}(2) &\cong \operatorname{lin\,span}
\left\{ \operatorname{ad}E,\operatorname{ad}H,\operatorname{ad}F\right\} \subseteq \mathfrak{gl}(3)
\end{align*}

Dear @fresh_42, thank you so much from the bottom of my heart for your clarification,

Please, the last question ( i get the answer but i would like to know in general) how we get this matrix, i mean what is its entries? ( I know the relation of E, H and F, but how we put the numbers inside the matrix)

$$
\operatorname{ad} E=\left(\begin{array}{ccc}
0 & -2 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{array}\right)
$$

thanks in advance,

To write a matrix we need
a) a linear function
b) the vector spaces this function maps from one to the other
c) bases for these vector spaces, which must not only span the vector spaces and be linearly independent but are also ordered, i.e. the basis vectors must be enumerated.

We have a) ##\operatorname{ad}E## and b) ##\operatorname{ad}E\, : \,\mathfrak{sl}(2)\rightarrow \mathfrak{sl}(2),## i.e. the vector spaces are ##\mathfrak{sl}(2)## in both cases. We also have a basis of ##\mathfrak{sl}(2),## namely ##H,F,E.##

So all that's left to know is an order. Normally, we would start with an order, say ##v_1,v_2,v_3## and write the matrix of ##\operatorname{ad}E## as ##(\operatorname{ad}E(v_1),\operatorname{ad}E(v_2),\operatorname{ad}E(v_3))## expressed as column vectors according to the basis ##(v_1,v_2,v_3).##

But in this case, you already have written the matrix. Let's see what this means for our basis.
The first column vector of ##\operatorname{ad}E## is the zero vector. So we can choose ##v_1=E## since ##\operatorname{ad}E(E)=[E,E]=0.## For the second column ##\operatorname{ad}E(v_2)## we have ##\operatorname{ad}(E)(v_2)=-2v_1.## Hence, ##v_2=H## does the job since ##\operatorname{ad}E(H)=[E,H]=-[H,E]=-2E=-2v_1.## The same with the third column and ##v_3=F.## Here we have ##\operatorname{ad}E(v_3)=v_2## and we can choose ##v_3=F## since ##\operatorname{ad}E(F)=[E,F]=H=v_2.## So our ordered basis is ##(v_1,v_2,v_3)=(E,H,F)## according to which we have written the matrix of ##\operatorname{ad}E.##

Please note, that ##\operatorname{ad}## itself is also a linear transformation. It maps the vector space ##\operatorname{ad}(\mathfrak{sl}(2))## into the general linear Lie algebra ##\mathfrak{gl}(\mathfrak{sl}(2))=\mathfrak{gl}(3).## This is a map from a three-dimensional vector space into a nine-dimensional vector space. It maps the basis ##(\operatorname{ad}E,\operatorname{ad}H,\operatorname{ad}F)## onto the ##3\times 3## matrices you found in post #1. They do not span ##\mathfrak{gl}(3).## They span only a three-dimensional subspace and we have
$$
\mathfrak{sl}(2) =\operatorname{lin \,span} \{E,H,F\} \cong \mathfrak{ad}(\mathfrak{sl}(2))=\operatorname{lin \,span} \{\operatorname{ad}E,\operatorname{ad}H,\operatorname{ad}F\} \subseteq \mathfrak{gl}(3)
$$

@fresh_42 Thank you, thank you, words cannot describe how grateful I am to you.

Dear @fresh_42 , I am so sorry for bothering you,

please, why you put x1=1, x2=1, x3=1, here, I know it is above, but in general why?
y1, y2, y3 have different values, but xi are the same

$$
K\left(X_1, Y_1\right)+K\left(X_2, Y_2\right)+K\left(X_3, Y_3\right)=4 \cdot 1 \cdot \frac{1}{4}+8 \cdot 1 \cdot \frac{1}{8}+4 \cdot 1 \cdot \frac{1}{4}=3
$$

thanks in advance,

HDB1 said:

Dear @fresh_42 , I am so sorry for bothering you,

please, why you put x1=1, x2=1, x3=1, here, I know it is above, but in general why?
y1, y2, y3 have different values, but xi are the same

$$
K\left(X_1, Y_1\right)+K\left(X_2, Y_2\right)+K\left(X_3, Y_3\right)=4 \cdot 1 \cdot \frac{1}{4}+8 \cdot 1 \cdot \frac{1}{8}+4 \cdot 1 \cdot \frac{1}{4}=3
$$

thanks in advance,

Please correct me if I'm wrong. I assume you refer to post #9. Since we deal with ##3\times 3## matrices, i.e. nine entries, it is better to have a numbered basis, so I set ##X_1=E\, , \,X_2=H\, , \,X_3=F.##

Say we have two arbitrary vectors ##X=x_1X_1+x_2X_2+x_3X_3=x_1E+x_2H+x_3F## and ##Y=y_1X_1+y_2X_2+y_3X_3=y_1E+y_2H+y_3F## then
$$
K(X,Y)=\operatorname{trace}(\operatorname{ad}X \operatorname{ad}Y)=4x_1y_3+8x_2y_2+4x_3y_1\;(*)
$$
This is the general formula obtained by taking the matrices of ##\operatorname{ad}X## and ##\operatorname{ad}Y,## multiplied them, and finally taking the trace.

We need the dual basis of ##\{X_1,X_2,X_3\}## in order to calculate the Casimir element and in particular its trace. Let ##\{Y_1,Y_2,Y_3\}## be that basis. Duality means that ##K(X_i,Y_j)=\delta_{ij}\; (**).##

Hence I wrote the vectors ##Y_j## in the basis ##\{X_1,X_2,X_3\},## i.e. ##Y_j=y_{j1}X_1+y_{j2}X_2+y_{j2}X_3## and solved this linear equation system ##(**)## for the variables ##y_{ij}.## The result was that ##Y_1=(1/4)X_1\, , \,Y_2=(1/8)X_2\, , \,Y_3=(1/4)X_3.##

Finally, I go back to ##(*)## in order to compute ##K(X_i,Y_i).## The formula holds true for any vectors ##X,Y## expressed in the basis ##\{X_1,X_2,X_3\}.## But here we have
\begin{align*}
X_1=x_1X_1+x_2X_2+x_3X_3=1\cdot X_1 +0\cdot X_2+0\cdot X_3& \triangleq (x_1,x_2,x_3)=(1,0,0)\\
X_2=x_1X_1+x_2X_2+x_3X_3=0\cdot X_1 +1\cdot X_2+0\cdot X_3&\triangleq (x_1,x_2,x_3)=(0,1,0)\\
X_3=x_1X_1+x_2X_2+x_3X_3=0\cdot X_1 +0\cdot X_2+1-\cdot X_3&\triangleq (x_1,x_2,x_3)=(0,0,1)\\
Y_1=y_{11}X_1+y_{12}X_2+y_{13}X_3=(1/4)\cdot X_1+0\cdot X_2+0\cdot X_3&\triangleq (y_1,y_2,y_3)=(1/4,0,0)\\
Y_2=y_{21}X_1+y_{22}X_2+y_{23}X_3=0\cdot X_1+(1/8)\cdot X_2+0\cdot X_3&\triangleq (y_1,y_2,y_3)=(0,1/8,0)\\
Y_3=y_{31}X_1+y_{32}X_2+y_{33}X_3=0\cdot X_1+0\cdot X_2+(1/4)\cdot X_3&\triangleq (y_1,y_2,y_3)=(0,0,1/4)
\end{align*}
So our formula ##(*)\; K(X,Y)=4x_1y_3+8x_2y_2+4x_3y_1## becomes
$$
K(X_1,Y_1)=4\cdot 1\cdot (1/4)\, , \,K(X_2,Y_2)=8\cdot 1\cdot (1/8)\, , \,K(X_3,Y_3)=4\cdot 1\cdot (1/4)
$$
and the sum equals ##3,## the dimension of ##\mathfrak{sl}(2).##

Dear @fresh_42, thank you thank you , you are the best ever,

please I have a question, if we want to prove the lie algebra is semi simple, so, we have to prove that killing form is nondegenerate( its determinants does not equal zero), is it right?

so here we have : $$
K\left(X_1, Y_1\right)=3
$$Thanks in advance,

HDB1 said:

Dear @fresh_42, thank you thank you , you are the best ever,

please I have a question, if we want to prove the lie algebra is semi simple, so, we have to prove that killing form is nondegenerate( its determinants does not equal zero), is it right?

Yes. But non-degenerate means that if ##K(X,Y)=0## for all ##Y## then ##X=0## has to hold.
Let's see. We have ##K(X,Y)=0=4x_1y_3-8x_2y_2+4x_3y_1## for all ##Y=(y_1,y_2,y_3).##

Choose ##Y=(y_1,y_2,y_3)=(1,0,0).## Then ##0=K(X,Y)=4x_3## and so ##x_3=0.##
Choose ##Y=(y_1,y_2,y_3)=(0,1,0).## Then ##0=K(X,Y)=8x_2## and so ##x_2=0.##
Choose ##Y=(y_1,y_2,y_3)=(0,0,1).## Then ##0=K(X,Y)=4x_1## and so ##x_1=0.##

Hence, if ##K(X,Y)=0## for all ##Y## then ##X=(x_1,x_2,x_3)=0## has to hold.

(You also see that the characteristic different from ##2## of the scalar field is important! Otherwise, would ##4## and ##8## be zero divisors and we couldn't divide by them.)

fresh_42 said:

Yes. But non-degenerate means that if ##K(X,Y)=0## for all ##Y## then ##X=0## has to hold.
Let's see. We have ##K(X,Y)=0=4x_1y_3-8x_2y_2+4x_3y_1## for all ##Y=(y_1,y_2,y_3).##

Choose ##Y=(y_1,y_2,y_3)=(1,0,0).## Then ##0=K(X,Y)=4x_3## and so ##x_3=0.##
Choose ##Y=(y_1,y_2,y_3)=(0,1,0).## Then ##0=K(X,Y)=8x_2## and so ##x_2=0.##
Choose ##Y=(y_1,y_2,y_3)=(0,0,1).## Then ##0=K(X,Y)=4x_1## and so ##x_1=0.##

Hence, if ##K(X,Y)=0## for all ##Y## then ##X=(x_1,x_2,x_3)=0## has to hold.

(You also see that the characteristic different from ##2## of the scalar field is important! Otherwise, would ##4## and ##8## be zero divisors and we couldn't divide by them.)

Thank you so much, please, If we want to prove that ##sl(2)## is semi simple, should I use the all steps above in previous answer, I mean I get confused why you assume ##Y=(y_1,y_2,y_3)## in this way?

also, please bear with me, if characteristic is 2, what will happen?

HDB1 said:

Thank you so much, please, If we want to prove that ##sl(2)## is semi simple, should I use the all steps above in previous answer, I mean I get confused why you assume ##Y=(y_1,y_2,y_3)## in this way?

To prove that ##\mathfrak{sl}(2)## is semisimple we need to show that its maximal solvable ideal is zero. However, ##\mathfrak{sl}(2)## is a small world to live in. Only three dimensions. And it is simple, which means it has no ideals at all! Therefore it is sufficient to show that there are no proper ideals. No ideals, no radical. Hence assume ##\{0\}\neq I\subsetneq \mathfrak{sl}(2)## is an ideal and ##X=eE+hH+fF\in I-\{0\}.##
Then, since ##I## is an ideal:
\begin{align*}
I\ni [X,E]&=e[E,E]+h[H,E]+f[F,E]=2hE-fH\\
I\ni [2hE-fH,E]&=2fE
\end{align*}
If ##f\neq 0## then ##E\in I## and ##[E,F]=H\in I## and ##[H,F]=-2F\in I## hence ##\mathfrak{sl}(2)\subseteq I.## Thus ##f=0.## But then
\begin{align*}
I\ni [X,E]&=2hE
\end{align*}
and again ##E\in I## which is impossible by the same argument as before. Hence ##h=0.## But then we have ##X=eE## and we are again in an impossible situation. Conclusion: ##\mathfrak{sl}(2)## has no ideals other than ##\{0\}## and itself ##\mathfrak{sl}(2).## In particular, its radical is zero, and ##\mathfrak{sl}(2)## is semisimple. But we already knew it is even simple.

##\mathfrak{sl}(2)=\operatorname{lin \,span} \{E,H,F\}## so ##Y\in \mathfrak{sl}(2)## can be written ##Y=y_1E+y_2H+y_3F## which is in coordinates ##Y=(y_1,y_2,y_3).##

HDB1 said:

also, please bear with me, if characteristic is 2, what will happen?

This is a very good question. I'd say "hell breaks loose".

We have no signs in fields with characteristic ##2,## ##+1=-1.## This means the trouble already starts with the definition. We have defined ##[x,x]=0.## So
\begin{align*}
0=[x+y,x+y]&=[x,x]+[x,y]+[y,x]+[y,y] =[x,y]+[y,x] \Longrightarrow [x,y]=-[y,x]=[y,x]
\end{align*}
and we have an abelian multiplication. This has little to do with Lie algebras as we know it. We can still define e.g.
$$
\mathfrak{sl}(2,\mathbb{F}_2)=\left\{\begin{pmatrix}a&b\\c&a\end{pmatrix}\,|\,a,b,c\in \mathbb{F}_2\right\}
$$
but this would consist of only four matrices. The entire idea of anti-commutativity will be lost.

I bet that mathematicians have dealt with it, but I don't know any references. There are of course more complex fields of characteristic two than ##\mathbb{F}_2=\{0,1\},## e.g. function fields. However, I haven't met this very dark part of Lie theory.

Lie algebras naturally occur in physics where they a) originated from and b) characteristic zero is the dominant property. So any other case is of pure algebraic interest.

Dear @fresh_42 , Thank you so much for the clarification, I really appreciate your help and time, thank you thank you from the bottom of my heart,

I have a question about this, please, if we want to prove that ##\mathfrak{s l}(2)## is semi simple, by using:
##L## is semi simple if its killing form is nondegenerate,

how we can do this, please?Thanks in advance,

HDB1 said:

Dear @fresh_42 , Thank you so much for the clarification, I really appreciate your help and time, thank you thank you from the bottom of my heart,

I have a question about this, please, if we want to prove that ##\mathfrak{s l}(2)## is semi simple, by using:
##L## is semi simple if its killing form is nondegenerate,

how we can do this, please?Thanks in advance,

Well, no ideals therefore no solvable ideal therefore radical equals zero is faster, but as you like.

The Killing form is non-degenerate if
$$
K(X,Y)=0 \text{ for all }Y\in \mathfrak{sl}(2) \;\Longrightarrow \;X=0
$$
So it's clear what to do. Assume we have ##X=x_1 E+x_2 H+x_3 F \in \mathfrak{sl}(2)## such that ##K(X,Y)=0## for all ##Y=y_1E+y_2H+y_3F \in \mathfrak{sl}(2).## We already computed the Killing form of ##\mathfrak{sl}(2)## and it turned out to be
$$
K(X,Y)=K(x_1 E+x_2 H+x_3 F\, , \,y_1E+y_2H+y_3F)=\operatorname{trace}(\operatorname{ad}(X)\cdot \operatorname{ad}(Y))=4x_1y_3+8x_2y_2+4x_3y_1.
$$
Now, ##K(X,Y)=0## for all ##Y## means for ##Y_1=1\cdot E+0\cdot H+0\cdot F,## ##Y_2=0\cdot E+1\cdot H+0\cdot F,## and ##Y_3=0\cdot E+0\cdot H+1\cdot F,## in particular that
\begin{align*}
K(X,Y_1)=K(X,E)=0=4\cdot x_1 \cdot 0 +8\cdot x_2\cdot 0+4\cdot x_3\cdot 1= 4x_3 &\Longrightarrow x_3=0\\
K(X,Y_2)=K(X,H)=0=4\cdot x_1 \cdot 0 +8\cdot x_2\cdot 1+4\cdot x_3\cdot 0= 8x_2 &\Longrightarrow x_2=0\\
K(X,Y_3)=K(X,F)=0=4\cdot x_1 \cdot 1 +8\cdot x_2\cdot 0+4\cdot x_3\cdot 0= 4x_1 &\Longrightarrow x_1=0
\end{align*}
All coordinates ##x_1,x_2,x_3## of ##X## are zero, so ##X=0## and the Killing-form is non-degenerate.

Proceed by using the definitions. (And the calculation of the Killing form.)

Thank you so much, @fresh_42 ,