- #1
JD_PM
- 1,131
- 158
- TL;DR Summary
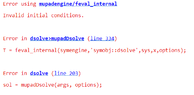
- I am trying to solve the following set of 5 first order ODEs with ICs but I get an error output "invalid ICs". What am I missing?
I am trying to solve the following set of 5 first order ODEs
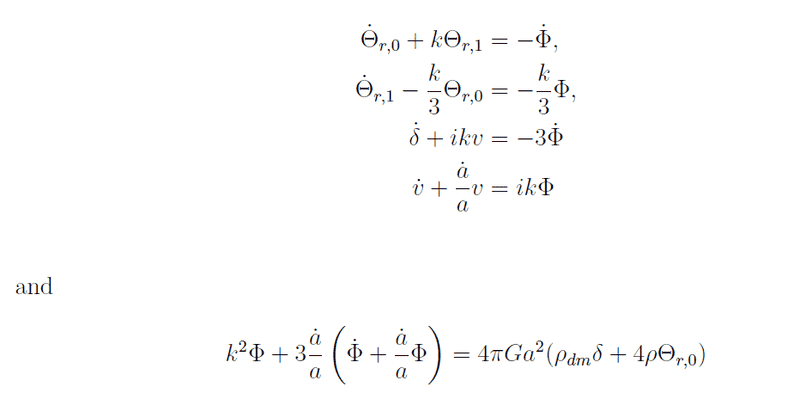
Where the variables are ##\Theta_0, \Theta_1, \Phi, \delta## and ##v##. The initial conditions (ICs) are
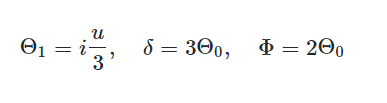
(Note that there is a typo in the above ICs; it is ##v## instead of ##u##). I am following this solved sample, following the exact same steps. However I get an error

Are these 3 ICs not enough?
Thank you!
Where the variables are ##\Theta_0, \Theta_1, \Phi, \delta## and ##v##. The initial conditions (ICs) are
(Note that there is a typo in the above ICs; it is ##v## instead of ##u##). I am following this solved sample, following the exact same steps. However I get an error
Are these 3 ICs not enough?
Thank you!