When Vehicle Power Dictates Acceleration - Comments

Greg Bernhardt submitted a new blog post

When Vehicle Power Dictates Acceleration


Continue reading the Original Blog Post.

Of your initial three points, only the first one is correct.

At any given velocity:
The force applied to the vehicle dictates the acceleration it gets;
The power applied to the vehicle dictates the force it gets;
Therefore, the maximum possible acceleration of the vehicle depends solely on the maximum power available for the vehicle.

At v=0 the second statement is completely false for any vehicle, and it is a very poor approximation for low speeds for automobiles. And the third is never correct, there are always other factors involved.

You do make a good point that not all vehicles produce torque as part of their operating mechanism.

For vehicles such as automobiles whose operating mechanism produces wheel torque, most of your arguments are specious. You could simply replace the word “power” with the word “torque” (or better yet “force”) and come up with the same argument for torque (or more generally for force) as being the primary quantity.

The one exception is the conservation of energy, which is a strong and general principle that should be understood.

The “anti torque” argument of your concluding section is also specious. Yes, you can rewrite wheel torque in terms of power, but for vehicles like automobiles you can also write power in terms wheel torque. The torque (or more generally the force) winds up being more closely related to acceleration.

Power is conserved. Acceleration is not conserved so it should not be too surprising that it is more directly related to non conserved quantities like torque or force.

Dale, you continue to miss the entire point here.

The question here is, given a set of parameters for your vehicle, which one do you care about for maximizing acceleration. Nobody, *nobody*, specifies a vehicle by tractive effort unless you're talking about a freight train. Rather, you have engine torque, horsepower, weight, etc. For the purpose of maximizing vehicle acceleration, the parameter you should care about is horsepower (more accurately, horsepower to weight). For acceleration at non-zero speeds, you should always be running the engine as close to peak power as possible, and to improve vehicle acceleration, you should always try to improve the power to weight ratio.

EDIT: Oh, and as far as the "conserved quantities" argument goes, you could easily reframe acceleration as being the rate of addition of kinetic energy. This makes it very clear that to maximize the rate of increase of kinetic energy, you need the greatest power possible.

cjl said:

The question here is, given a set of parameters for your vehicle, which one do you care about for maximizing acceleration. Nobody, *nobody*, specifies a vehicle by tractive effort

I agree with this statement, and if the statement were specified that way then it would be correct.

But that isn’t what he said and what he said is incorrect. He stepped away from your sound shopping advice to unsound physics.

cjl said:

you could easily reframe acceleration as being the rate of addition of kinetic energy.

Acceleration is not the rate of addition of kinetic energy. That is not merely reframing the question; it is a different question with a different answer.

This is something I've thought through quite a bit over the years. What I realized is that you have to look at it from the standpoint of what limits the acceleration, and it depends on conditions. There are three common limitations: 1) Traction, 2) Power, and 3) Wheelstand.

Here's the key: The vehicle can accelerate no quicker than the least of these three acceleration rates. Note that the second depends strongly on speed. So how large is each possible acceleration level? (I'm not going to worry about wheelstand here, by the way.)

Traction-Limited Acceleration Level: Here, all you need to know is the maximum available traction force, and the vehicle mass (barring aero drag, road grade, etc.). So the traction-limited acceleration level is straight from Newton's second law: a_TL=Fmax/m.

Power-Limited Acceleration Level: Here you are assuming that all the available power is going into acceleration (ignoring for now whether there is enough traction to do so). Since F=ma, and Pmax=Fv, then Pmax=mav. The power-limited acceleration level would be just a_PL=Pmax/(mv).

Now let's take an example. Let's say the car's mass m is 1500 kg (3300 lb), the maximum traction Fmax is 8000 N (1800 lbf), and the maximum power Pmax is 180 kW (241 HP) at the tire/pavement interface.

If you evaluated acceleration at 10 m/s (32.8 ft/s), the power-limited acceleration would be about 1.223 G’s, which there isn’t enough traction to accomplish (the tires spin first). The available traction would limit you to a_TL=0.544 G’s. So the maximum possible rate at 10 m/s is 0.544 G’s.

If you evaluated acceleration at 30 m/s (98.4 ft/s), the power-limited acceleration would be about 0.408 G’s, which is lower than the traction limited acceleration, still 0.544 G’s. So the maximum possible at 30 m/s is 0.408 G’s.

There is a critical speed in between those, where the traction-limited and power-limited acceleration are equal. This is where Pmax=Fmax*v_Crit, producing v_Crit=Pmax/Fmax. In our example, this critical speed is 22.5 m/s (73.815 ft/s).

So for this vehicle, the maximum acceleration below 22.5 m/s is a_TL=0.544 G’s. Above that, the maximum is a_PL=(180000 watts)/((1500 kg)*v), so the maximum possible acceleration decreases hyperbolically with speed.

What’s the takeaway? At low speed, very large traction forces would be needed to convey max power, so acceleration is limited by available traction. At high speeds, accelerating at the traction limit would require very large amounts of power, so acceleration is limited by power. The speed Pmax/Fmax divides the two regions.

Here is a plot of what I was describing. The max power could produce the dashed orange line, and the available traction could produce the dashed blue line. In actuality, acceleration is limited to the lesser of the two (the gray solid line).

@Dale :

I've been thinking long and hard about how to show you how your point of view is misleading, especially if you are addressing rookies in the field.

You are saying that all you need to create an acceleration at velocity ##v## is wheel torque because only forces are involved with accelerations;

I'm saying that you all you need to create an acceleration at velocity ##v## is wheel power because the power requirement is not the same at different velocities.

Both of these statements are true. But let's take a look at the same vehicle with a slightly different problem: Finding the maximum velocity.

Finding the maximum velocity is a pure «force» problem, just like acceleration. The tractive effort must be equal to the aerodynamic drag. Based on this, one can say:
$$T \propto v^2$$
And that is technically correct: The wheel torque ##T## must be proportional to the squared velocity.

But I say ¨Hold on!¨ There is also power involved. The wheel power ##P## must be equal to the drag power. This statement is the same as the previous one, but we multiply both forces by ##v##. This leads to:
$$P \propto v^3$$
Both of the above equations are true. But one of them conveys a lot more information than the other. The «torque» equation is misleading. A rookie will think that if he can put a gear ratio large enough, he will somehow get the wheel torque he wants from an energy source with a given torque. That is not true.

But with the «power» equation, he can assume that if he chooses the appropriate gear ratio, he can get the desired wheel torque AND accomplish that at the required velocity, as long as the energy source gives the required power.

The «power» equation implies the «torque» equation AND gives additional - and important - information.

I can assure you that your point of view will confuse more rookie than mine. I´ve been there, so did a lot of my peers at their beginnings. Sadly, even with a lot of experience, some still refuse to see the law of conservation of energy and pretend that only engine torque matters with acceleration, not engine power. And all of this is because they argue that «only wheel torque matters», which is directly linked to engine torque via the gearbox.

I guess what I´m saying is: Don´t feed the trolls.

jack action said:

You are saying that all you need to create an acceleration at velocity v is wheel torque

I would not say “all you need” because power and wheel torque are closely related and saying “all you need” is an oversimplification that misses a lot of important physics.

jack action said:

I'm saying that you all you need to create an acceleration at velocity v is wheel power

And this is clearly wrong. It is not “all you need”. As @Randy Beikmann clearly and correctly pointed out it is not even the limiting factor at low speeds.

jack action said:

Both of these statements are true.

I disagree, neither is true. The truth is that either “all you need” statement is myopic and misses the interplay between the various factors involved. The truth is that wheel power and wheel torque are closely related.

However, in the end it is undeniable that the quantity most directly related to acceleration is wheel torque, not power. I say undeniable, except that you did exactly that, you denied it! You are so embroiled in your black and white “all you need” that you make statements which are false and arguments which are specious.

jack action said:

But let's take a look at the same vehicle with a slightly different problem: Finding the maximum velocity.

For that problem I would unambiguously choose the power equation also. This is a different question and hence has a different answer. In that case power is clearly the more appropriate quantity to use and so I would use it.

jack action said:

I guess what I´m saying is: Don´t feed the trolls.

What I am saying is: teach physics!

I am uninterested in choosing sides in the ongoing debate amongst car enthusiasts. But here, on Physics Forums, we should teach correct physics.

Whether you like it or not, torque is an important concept in physics and cannot and should not be neglected when it is the most appropriate concept for the question at hand. This is not a political campaign where we have the torque party and the power party and the other party consists of trolls. This is physics where both torque and power are essential concepts and each have their legitimate place in describing the world. Torque is not always the most relevant quantity, nor is power.

jack action said:

@Dale :

Sadly, even with a lot of experience, some still refuse to see the law of conservation of energy and pretend that only engine torque matters with acceleration, not engine power.

That energy is conserved is indisputable, but where it goes depends on the situation. At low vehicle speeds (say 5 mph), your engine will not be able to run at maximum power Pmax, because if you put your right foot to the floor, the driving tires will spin until your engine goes to redline. At no engine speed would you be able to reach Pmax=T_Engine*omega, because the traction will limit the torque that can be developed. Plus, some of the energy the engine creates will go into the vehicle's kinetic energy, but some will be converted to heat at the tread as the tires slide against the pavement. There simply isn't enough traction to handle the force you would calculate at the tire/road interface in assuming Pmax there.

A good way to illustrate the difference is to calculate the time to accelerate from zero to a given speed, using constant power vs. Newton's laws. Suppose I want to calculate the time for the car I used above to go from 0-45 mph (66 ft/s). If I did so setting power = Pmax, and set final kinetic energy (0.5*m*v^2) equal to work done (Pmax*t), I would get t=1.69 seconds. If I used Newton's laws, then the final velocity equals the traction-limited acceleration multiplied by the time, or v = a_TL*t. Solving, this produces t=v/a_TL, which in this case is 2.51 seconds, and is the actual answer. Why is the actual answer so much slower than the power-based calculation? Because applying the entirety of Pmax to accelerating the vehicle is impossible at low speeds, as noted above.

I would never advise anyone to always favor the energy approach over Newton's laws, or vice versa - in fact you must consider both factors to ensure a correct solution. Both should be considered, and the result should be the same. If they're not, you're missing something. In this case it would be that "power being conserved" is only applicable if there are no factors involved that dissipate some of it as other forms of energy, in this case heat.

Randy Beikmann said:

I would never advise anyone to always favor the energy approach over Newton's laws, or vice versa

Well said!

Randy Beikmann said:

because the traction will limit the torque that can be developed

What if there is no traction limit? Well the passengers inside the vehicle will die if the acceleration is too great. That is another limit.

What if there are no passengers inside? Well the mechanical components will break apart under a certain acceleration level. That is another limit.

The problem right now is that the question is not about what are all the possible limits of acceleration, it is about a single one: Is power or torque a better indicator of acceleration? Google will send all the users typing this question to the insight I wrote and other similar threads because they have the terms ¨power¨, ¨torque¨ and ¨acceleration¨ in it.

Let me show you the problem at hand. If you discuss with a «torque» person and ask him which of 2 engines you have can produce the largest acceleration knowing that you have the exact same transmission in both cases, you can only change the differential gear ratio. He will say ¨Acceleration depends on wheel torque, so show me the torque of the engines¨:


After seeing that, he will suggest the blue engine. Not asking you anymore questions. But you say ¨Some people look only at the engine power, what do you think about that?¨:


He will answer back ¨It doesn´t matter, only torque creates acceleration¨. So you tell him ¨But they insist, they compare the power curves over the RPM/RPM_max ratio¨:


He will answer ¨It doesn´t prove anything. See the torque curves with that same condition¨:


¨There, those scientists don´t know anything about real life. It´s only theory.¨ And he will add ¨Besides, go on PF and you´ll see that scientists don´t all agree on that: some say that only torque matters, just like me.¨

This is the implication of not choosing carefully your words about the subject. If you think I am creating something out of nothing, see this thread where the OP cannot stop opposing engine builders with scientists. Even his nickname is Moretorque for pete´s sake. You can find hundreds of discussions like this over the net and these discussions were going on before the net existed.

I don´t care about any other limits (traction, human tolerance, material resistance, etc.) that can lower the threshold of maximum acceleration. Given those numbers, it must be very clear to anyone that the orange engine can produce way more acceleration than the blue one. There are no ´if´ or ´but´, or any kind of discussion possible about it.

Otherwise, one could also argue that acceleration is not proportional to the force as well, since ##F = v\frac{dm}{dt} + ma##. So even if there is a force, the acceleration could be zero, therefore you cannot assume proportionality. Even if it´s true, it is a really dishonest - and not helpful at all - argument.

Don´t feed the trolls.

As much as I hate to step into an emotional internet discussion, I wonder if there is just a communication issue going on here. Are we talking about instantaneous acceleration at a particular engine's torque peak, or are we talking about accumulated (integrated) acceleration, like trap speed at a drag strip?

jack action said:

The problem right now is that the question is not about what are all the possible limits of acceleration, it is about a single one: Is power or torque a better indicator of acceleration? Google will send all the users typing this question to the insight I wrote and other similar threads because they have the terms ¨power¨, ¨torque¨ and ¨acceleration¨ in it.

If the question is whether power or torque is "a better indicator of acceleration", then I'm afraid there is no general answer. It depends on the full question/problem definition - there are always "if's" that will determine the answer. It's like when someone asks you, "What's the best car to buy?" The answer must be qualified by your purposes, budget, etc.

If the problem allows any transmission to be used, including a CVT, then the answer is (assuming no losses) that max engine power is more important than engine torque, since you can hold the engine at its peak power speed at "any" vehicle speed (that is actually stretching it, since even a CVT can't produce an infinite range of ratios), whether you can utilize it or not. But a properly matched fast-shifting DCT could keep the engine speed near enough to the peak power speed so that it's not that much different than the CVT. Now, if the question stipulates low vehicle speeds, all that matters is that the engine can produce enough power to produce the force at the tread that fully utilizes the tires' traction, and the maximum amount of power available (Pmax) is not important.

If prepping a drag racer, launch is the most important aspect - if you get a slow start, it takes a huge amount of power later in the run to try to catch up. I would first concentrate on traction (force capability), because the launch is traction-limited. Then I would set the transmission and final drive gear ratios to multiply the engine torque and produce enough axle torque to use that traction. But it does not take that much power at launch, since P=Fv, assuming no losses. A lower-power car with correct gearing and tires can easily beat a high-power car that is incorrectly set up.

As to how to guide the discussions and correct the wrong conclusions by gearheads out there, my solution was to write a book that (IMHO) clearly and correctly explains all this in detail. Smart gearheads do use physics.

jack action said:

Greg Bernhardt submitted a new blog post

When Vehicle Power Dictates Acceleration
View attachment 234244Continue reading the Original Blog Post.

Sure the acceleration depends on the power but it's not the maximum power available, it's the power available at that velocity.

sandy stone said:

Are we talking about instantaneous acceleration at a particular engine's torque peak, or are we talking about accumulated (integrated) acceleration, like trap speed at a drag strip?

We are talking about an acceleration at a given velocity (other than zero). More precisely, over a speed range.

Randy Beikmann said:

Now, if the question stipulates low vehicle speeds, all that matters is that the engine can produce enough power to produce the force at the tread that fully utilizes the tires' traction, and the maximum amount of power available (Pmax) is not important.

Pmax might not be important, but power still is. If the maximum friction force (or any other limiting factor you can think of) allows for, say, 10 000 N at a speed of 1 m/s, knowing the torque produced by the engine alone won´t be enough information, no matter the gearing or tire radius. You have to make sure the engine produces enough power, i.e. the exact same amount needed at the wheel. It doesn´t even matter how much torque it produces and at what rpm. It doesn´t even matter if it is a combustion engine or not. All that matters is how much power it produces.

The acceleration needed at the wheel from my example will be 10 000 N divided by the mass of the vehicle (ignoring rotational inertia to keep it simple). What do I need from the engine? 10 000 W (= 10 000 N X 1 m/s). That´s all you need to know. That is the only thing to remember from the insight I wrote. For more detailed information, I wrote 8 pages about it on my website to explain the acceleration simulator I build (see my signature); It is too much info to fit in a single insight which is meant to answer one simple question.

jack action said:

The acceleration needed at the wheel from my example will be 10 000 N divided by the mass of the vehicle (ignoring rotational inertia to keep it simple). What do I need from the engine? 10 000 W (= 10 000 N X 1 m/s).

I think this is getting to the heart of the matter. As soon as you specify a particular speed, then torque and power are essentially two sides of the same coin, speed being the conversion factor. This whole discussion is similar to arguing whether a pressure differential in a pipeline causes a flow, or whether a flow causes a pressure differential. I would say neither, or both, if you like. They just happen together. In the same way, 10 000 N at 1 m/sec IS 10 000 W, and it's a matter of convenience (or personal opinion) which is considered the primary quantity and which is the derived quantity. Again, only because the speed is specified.

sandy stone said:

This whole discussion is similar to arguing whether a pressure differential in a pipeline causes a flow, or whether a flow causes a pressure differential.

Funny that you mention pressure differential and a flow. If you had a hydraulic motor powering my vehicle, I don´t know what would be the its pressure differential or volumetric flow rate, but the combination of both would have to produce 10 000 W. This is the only characteristic required to be sure I can produce the desired force (or acceleration) at the given velocity. It would be a mistake to think that only the pressure is relevant because that is what will cause the wheel torque. Any pressure can produce that torque, as long as it has the appropriate volumetric flow rate.

jack action said:

We are talking about an acceleration at a given velocity (other than zero).

I am certainly not excluding zero velocity. You would certainly like to exclude it since it makes your claim obviously wrong, but I do not consent to the limitation.

jack action said:

Is power or torque a better indicator of acceleration?

Let’s examine it for the simple lossless case:

Wheel torque is always proportional to acceleration with a simple constant of proportionality.

Power is related to acceleration by a proportionality which is not constant.

At v=0 power becomes infinite, but acceleration and wheel torque maintain their standard proportionality.

At small but nonzero speeds power becomes arbitrararily large but acceleration and wheel torque do not.

Wheel torque and power are not independent but are closely related to each other by speed.

The combination of power and speed that is related to acceleration is itself proportional to wheel torque with the above simple constant of proportionality.

Wheel torque is proportional to acceleration from rest, power is not.

With a CVT power is constant, but both wheel torque and acceleration are not and at all times the wheel torque is proportional to the acceleration.

With a typical powertrain in a fixed gear the peak wheel torque often occurs at lower speeds than the peak power, the peak acceleration occurs at the speed of the peak wheel torque not the peak power.

For constant wheel torque acceleration is constant, while power is not.

So clearly, wheel torque is more directly related to acceleration than power. So what is the value of power: first it is the primary criterion to use when selecting an engine. Second, power is conserved but torque is not, so the relationship between wheel torque and engine torque is not as simple as the relationship between wheel power and engine power. Third, power is more relevant for determining peak speed. I am sure there are many other examples where power is more directly relevant than wheel torque, but acceleration is obviously one of the exceptions where wheel torque is more directly relevant.

jack action said:

Given those numbers, it must be very clear to anyone that the orange engine can produce way more acceleration than the blue one.

Sure, and it does so precisely by converting that engine power into greater wheel torque. As I said above, power is the primary criterion for selecting an engine. The wheel torque is not independent of the engine power, but the wheel torque remains the quantity that is more directly related to acceleration.

@Dale , you know I agree with you on every sentence you write because, you said it yourself more than once, we basically say the same thing with different words. The ones I like from your last post are these ones:

Dale said:

The wheel torque is not independent of the engine power, but the wheel torque remains the quantity that is more directly related to acceleration.

I like how you use the double negative. Instead of saying «is dependent of», you say «is not independent of». I prefer the positive version: Acceleration depends on wheel torque and wheel torque depends on wheel power, which is the same as engine power (not considering inefficiencies). And the reason why I can so easily jump to «acceleration depends on power» when considering a vehicle is because the speed range for any vehicle design is fixed. A passenger car has one, a tractor has another one, a race car another one. The speed range is a given, always.

This is why I can relate directly the power curve of an engine to its acceleration as long as the speed range are comparable. Knowing that there are so many people out there who strongly argue that «acceleration depends on wheel torque and wheel torque depends on engine torque», therefore «acceleration depends on engine torque», don't you think my choice of words are better suited to convey the science behind the phenomena? Those people are right with their statement by the way, it just doesn't take into account the speed change associated with the acceleration increase.

As for the difficulty you have about ##v=0##, I will quote another insight written by @anorlunda :

Underlying Assumptions and Limitations

Really there is only one assumption behind Ohm’s law; linearity. Not in the mathematical sense, but rather that a graph of voltage versus current shows an approximately straight line in a given range.

There are always limits to the range even though they may not be explicitly mentioned. For example, at high voltages breakdown and arcing can occur. At high currents, things tend to melt. In the old days, we said that real-world resistance can not be zero. But now we know that superconductors are an exception to that rule. ##R=0## is OK for superconductors.

Students often forget that limits exist. A frequent (and annoying) student question is, “So if ##I=V/R## , what happens when ##R=0##. Ha ha, LOL.” They think that disproves the “law” and thus diminishes the credibility of science in general. Their logic is false.

Reference https://www.physicsforums.com/insights/ohms-law-mellow/

jack action said:

@Dale , you know I agree with you on every sentence you write

Even this one?

Dale said:

So clearly, wheel torque is more directly related to acceleration than power

If so then state it clearly and if not then you need to address my specific justifications for that statement.

jack action said:

Acceleration depends on wheel torque and wheel torque depends on wheel power, which is the same as engine power (not considering inefficiencies).

I am fine with that. Engine power is the start, wheel torque is the end. Why is it so hard for you to admit that the end is more directly related to the result than the beginning? That should be obvious.

Dale said:

Even this one?If so then state it clearly and if not then you need to address my specific justifications for that statement.

Dale said:

So clearly, wheel torque is more directly related to acceleration than power.

If so then state it clearly and if not then you need to address my specific justifications for that statement.

In a pure sense, your statement will be true in any case (like when ##v=0##, for example). If you specified some context (like specifying acceleration over a speed range), then you cannot distinguish which of wheel torque or wheel power is more influential on acceleration. My text do specified the limits and context for my statement. Furthermore, I wanted to show that the statement is also true even if there is no wheel torque.

Dale said:

I am fine with that. Engine power is the start, wheel torque is the end. Why is it so hard for you to admit that the end is more directly related to the result than the beginning? That should be obvious.

Like I said above, in the specific case presented, they are equivalent and that is if wheel torque is present. So it ends up to be about which words you want to use to convey the message.

Why do I choose these words? Because I know my audience. I know what they read/heard before and where they get confused. I know the words they need to hear such that they come to the right conclusions. Most importantly, I know what words they don't need to read/hear, because it would only add to their confusion.

When you say «torque» (even if you specify «wheel torque»), they hear «engine torque». Once the torque requirement is fulfilled, most people failed to see the power requirement that must also be fulfilled. Somehow, the force concept is easier to «see» than power for physics newbies. Probably because you can feel a force but not power.

Finally, when the power requirement is fulfilled, the torque requirement is automatically fulfilled (at the desired velocity, that is). It makes things so much easier (no need to know the wheel radius or gear ratios). You should see the nightmare of calculations that some people do when using torque and RPM instead of power. It is very discouraging and it contributes to the hatred of math found in the general population. When I understood how easy it can be, I felt like a kid learning a magic trick!

At the risk of intervening in an apparent theological war, does it help to state that Power is a derived unit from Force (Torque), Speed, and Time?
That might even make it easier to explain to non-physicists.

jack action said:

In a pure sense, your statement will be true in any case

Excellent. I am glad you agree.

jack action said:

in the specific case presented, they are equivalent and that is if wheel torque is present. So it ends up to be about which words you want to use to convey the message.

In the many cases where they are equivalent then it is indeed merely a choice of words. However, I carefully chose examples where they were not equivalent. Since they are not always equivalent, it is not always just a stylistic choice.

Dale said:

However, I carefully chose examples where they were not equivalent. Since they are not always equivalent, it is not always just a stylistic choice.

Agreed.

Let me show you how people do the calculations when they focus on torque (I've been there). First they go for your simple equation:
$$ma = \frac{T_w}{r}$$
What is my wheel torque at velocity ##v##? Let's find out the engine rpm ##\omega_e##:
$$\omega_e = G_r\frac{v}{r}$$
Where ##G_r## is the gear ratio. Then, let's find the engine torque at the given engine rpm by examining the torque-rpm curve. Once you know the engine torque, we find the wheel torque:
$$T_w = G_r T_e$$
Finally we go back to our original equation and determine the acceleration. But is it the maximum acceleration we can get? The only way to be sure is to repeat the process with other gear ratios, build a table and compare acceleration values. Then I can choose which gear ratio is better suited to get maximum acceleration. But as I increase my speed the acceleration is always lower than at lower speeds. How do I know if this lower speed acceleration is the maximum I can get? Let's try another gear ratio, then. In the end, it is just how patient you are when it comes to try an infinity of possibilities, gear ratio-wise.

Yes, they are still people doing it this way. Essentially, they are solving the following equation, one set of brackets at a time:
$$ma = \frac{\left(G_r T_e\right)}{\left(\frac{\omega_e}{G_r}r\right)}\left(\frac{\omega_e}{G_r}\right)$$
It is extremely messy and it shows that you are not understanding something about physics. What I want them to see is:
$$ma = \frac{P_w}{v}$$
and because:
$$P_w = P_e$$
Then you can simply say:
$$ma = \frac{P_e}{v}$$
No need to convert velocity to angular velocity. Just convert your power-rpm curve to a power-velocity curve, and where you have the most power, you know you have the most acceleration possible at that speed. Once you're satisfied with this, then find out what gear ratios and wheel radius combination you need.

Here is a real life question I had from one of my website reader (yes, even after he read my website where I don't focus on gear ratio or tire radius):

I would like to know what factors you take into account when selecting gear and diff ratios for performance applications.

I only have minimal manufacture specifications (weight, weight distribution, frontal area, rolling resistance) and a simple power curve to go off. I also have a speed trace of the track it would be going around.

The current list of factors I am using to derive and tune ratios are:

-Acceleration force per gear. (accounting for resistive forces I.e. drag)

-Tire grip *Wheel Spin* (accounting for vertical forces on the axel)

-RPM drop and where in the powerband it drops to

-Short shifting

I was wondering if there were any major factors I am overlooking and should look into while selecting ratios.

I have attached my main tool if you have time to look at it. I appreciate that you’re probably quite busy and would completely understand if you didn’t have the time. But even a few pointers would be world of help.

This came with an Excel spreadsheet filled with the tables mentioned above, and more. He is obviously drowning in numbers. This was my answer:

The basic concept to remember is that, for any speed, the acceleration is proportional to wheel power.

Since power varies with RPM, you want to coincide the RPM where you get the maximum power with the speed where you spend the most time accelerating. Say you know you spend a lot of time accelerating between 150 and 200 km/h, then you should have one gear ratio that gives you peak power RPM when you are at 175 km/h. If you spend most of your time in that speed range, you may also want to set the lower and higher gear ratios closer to that ideal ratio. This will increase your average power in that speed range (closer to peak power).

This is what is shown in the next figures. It is actually based on the numbers from your attached file.

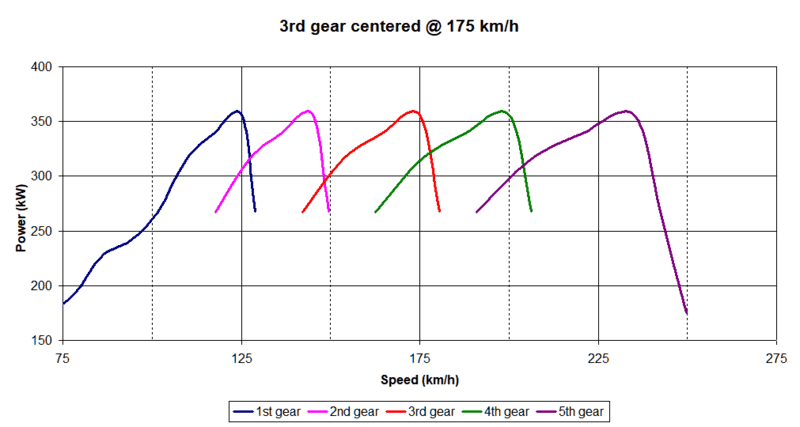
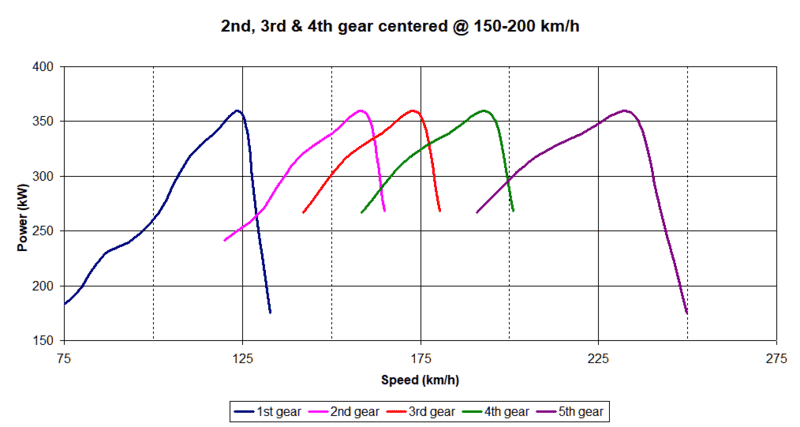
Wherever the lines crosses, these are your ideal shift points. You can see how the average power (between shift points) in the 150-200 km/h range is greater in the second figure, compared to the first figure. Of course, this is only an example, and the power lost at 130 and 200 km/h might be unacceptable. In such case, you either have to set a smaller overall speed range by bringing closer the 1st & 5th gear ratios (i.e. less power at low speed and a lower top speed possible) or you can add gear ratios to fill the voids (i.e. a 7-speed gearbox is required). Note that as you increase the number of gear ratios within a given speed range, you set the average power closer to the peak power (but shifting may cause some losses and/or get more complicated).

It is all about compromises.

The answer I got back was:

This is great, thank you so much! You gave me a lot of insight into the topic and I hadn't thought of it that way.

Nobody thinks of it that way when they are new at this. Too many even refuse to do otherwise as they get experience. Why? Because they focus on «acceleration means torque».

Jack, the example you showed here gave valuable insight to the user of your website, especially since it was applied to a specific situation. You used the concept of "power flow" through the driveline to simplify the problem of choosing gear ratios, using a systematic way to do it instead of trial and error. The plots showed how changing the grouping of gear ratios could more closely approximate a "constant power" relationship across a certain range of vehicle speeds.

I don't believe the article in "Insights" did justice to the way you explained things here. Now I better understand what you were after.

I do believe, though, that comparing alternate methods is very valuable in gaining insight. If things had started off with you teaching him how to do it by following the power through the driveline (rather than torque and force), he never would have appreciated the way it made things easier for this purpose. Initial frustration is a good motivator.

For some other purposes, I do still like plotting the acceleration capability vs. speed, including the case where only power limits it. That makes it evident that, even ignoring aerodynamic drag, the capability to accelerate diminishes with increasing speed. Also, if you need the performance envelope of a vehicle on a road course to do simulations, you can express it in terms of longitudinal and lateral accelerations (or forces), but not power since it does not enter into lateral acceleration.

The performance envelope might come in handy for your user's problem of matching gearing to a road course. Besides "smoothing" the power delivery in a specific speed range, he might also want to make sure he doesn't have to shift while accelerating out of a critical corner.

Randy Beikmann said:

I do still like plotting the acceleration capability vs. speed, including the case where only power limits it. That makes it evident that, even ignoring aerodynamic drag, the capability to accelerate diminishes with increasing speed.

That is why I prefer ##ma = \frac{P}{v}## rather than ##ma = \frac{T}{r}##. With the torque equation, it leaves the impression that you can get any level of acceleration, at any speed. With the power equation, you clearly see that the acceleration will decrease as the speed increases.

Thank you @jack action for your Insight article and also @Randy Beikmann and @Dale for your contributions to this discussion. I have long had a confusion about why people talk about both power and torque, and the relationship between the two, and had never found time to go into it enough to understand the role they play in the context of a motorised vehicle. This discussion finally cleared it up for me, especially Randy's graph on page 1!

(What ? no Latex in Insights comments ?)

Well of course we are free to choose tire radius r, when we build the vehicle.
We could select gears and wheel size to make torque and thrust numerically equal just to simplify the algebra.
That'd make acceleration = Torque/Mass

Radians per second X r is velocity
and Torque X radians per second is power
Power, velocity and Torque form a triad
so if you know any two you you know the third.
So to argue that using one is "better " than using the other is pointless.

""The radius r implies a transformation where power is kept constant,"
How ?
No more than "the energy source must be set to its maximum power – during the entire velocity range – to ensure that the vehicle will get its maximum possible acceleration throughout that velocity range" implies constant power.
Both those assumptions would require an infinitely variable transmission, and one of those is not assumed." implies it.

For any real engine torque and power are both functions of RPM(velocity)

so the choice of approaching it from power or torque is a personal preference, nothing more.

Acceleration is the key to drag racing
So
Let's assume distance s and use the familiar equation of motion s=(1/2) at^2 to figure time
where
distance = s
acceleration = a
time = t
velocity = v
power = P

We could set distance = 1320 feet but it's cleaner to just use the symbol "s"..

s= (1/2) at^2
time t = sqrt(2s/a)
obviously to minimize t you maximize a
since i chose gears and wheel radius to make torque equal thrust,
a= Torque/m
which makes time t = sqrt(2s X m/Torque)
and i can lump constants to get
time t = K/sqrt(Torque)
but Torque is not a constant, it's a function of engine rpm(velocity), so a proper solution involves integration.

Since P = mav
a = P/mv
substituting that into s= (1/2) at^2

s = (1/2) (P/mv) X t^2
t = sqrt(2s X mv/P)
again i can lump constants
t = K X sqrt (v/P)
Neither v nor P is constant (neither was Torque)

so you have a choice of which function to integrate, Torque or the function v/P

Torque and Power are readily available from the engine's performance curves, but v will have to be written as a function of torque and time .

I just don't understand your anti-Torque stance.

What ? no Preview in Insights Comments ?

old jim

? All those previous comments showed only after i posted mine.
This INSIGHTS board needs some serious software work.

jim hardy said:

(What ? no Latex in Insights comments ?)

Should be fixed in a month or two. Comment in the forums threads.

I've not read the prior comments , but certainly would have read them before commenting if they'd shown,

so if my remarks are repeat of somebody else's please excuse me.. I'll find them after a while.

No response necessary - i'll catch up...

old jim

Greg Bernhardt said:

jim hardy said:

(What ? no Latex in Insights comments ?)

Should be fixed in a month or two. Comment in the forums threads.

Thanks, Cap'n !

Torque (lb ft) versus speed (mph) versus gear for a 2001 Hayabusa (I own one of these). The crossing points of the lines are the ideal shift points. Peak torque in 1st gear translates into about 1.2 to 1.3 g acceleration (depending on rider weight and weight of gasoline in the tank), at which point it's wheelie limited unless the rider sit and leans forward (otherwise the bike tends to lift the front tire at around 40 to 45 mph if at full throttle).

Huh. That graph makes me wonder why 5th gear even exists. There's almost no time in which you'd want to be in 5th.

Tom.G said:

At the risk of intervening in an apparent theological war,

That's exactly what this thread is. It's big-endians and little-endians all over again, in search of a solutions to a problem that's not be properly specified. With a very few exceptions, the answer is that a good bigg'un beats a good little'n.

I don't know how I boarded this particular train but I only looked at the posting dates when I bumped into the lovely @jim hardy 's name. I bet he'd have a good laugh about this. His last post was in 2019!.