Why the Quantum | A Response to Wheeler’s 1986 Paper
Wheeler’s opening statement in his 1986 paper, “How Come the Quantum?” holds as true today as it did then [1]
The necessity of the quantum in the construction of existence: out of what deeper requirement does it arise? Behind it all is surely an idea so simple, so beautiful, so compelling that when — in a decade, a century, or a millennium — we grasp it, we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?
In this Insight, I will answer Wheeler’s question per its counterpart in quantum information theory (QIT), “How come the Tsirelson bound?” Let me start by explaining the Tsirelson bound and its relationship to the Bell inequality, then it will be obvious what that has to do with Wheeler’s question, “How Come the Quantum?” The answer (the Tsirelson bound is a consequence of conservation per no preferred reference frame (NPRF)) may surprise you with its apparent simplicity, but that simplicity belies a profound mystery, as we will see.
The Tsirelson bound is the spread in the Clauser-Horne-Shimony-Holt (CHSH) quantity
\begin{equation}\langle a,b \rangle + \langle a,b^\prime \rangle + \langle a^\prime,b \rangle – \langle a^\prime,b^\prime \rangle \label{CHSH1}\end{equation}
created by quantum correlations. Here, we consider a pair of entangled particles (or “quantum systems” or “quantum exchanges of momentum”). Alice makes measurements on one of the two particles with her measuring device set to ##a## or ##a^\prime## while Bob makes measurements on the other of the two particles with his measuring device set to ##b## or ##b^\prime##. There are two possible outcomes for either Bob or Alice in either of their two possible settings given by ##i## and ##j##. For measurements at ##a## and ##b## we have for the average of Alice’s results multiplied by Bob’s results on a trial-by-trial basis
\begin{equation}\langle a,b \rangle = \sum (i \cdot j) \cdot P(i,j \mid a,b) \label{average}\end{equation}
That’s a bit vague, so let me supply some actual physics. The two entangled states I will use are those which uniquely give rise to the Tsirelson bound [2-4] , i.e., the spin singlet state and the ‘Mermin photon state’ [5]. The spin singlet state is ##\frac{1}{\sqrt{2}} \left(\mid ud \rangle – \mid du \rangle \right)## where ##u##/##d## means the outcome is displaced upwards/downwards relative to the north-south pole alignment of the Stern-Gerlach (SG) magnets (Figure 1).
 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
This state obtains due to conservation of angular momentum at the source as represented by momentum exchange in the spatial plane P orthogonal to the source collimation (“up or down” transverse). This state might be produced by the dissociation of a spin-zero diatomic molecule [6] or the decay of a neutral pi meson into an electron-positron pair [7], processes which conserve spin angular momentum. For more information about the spin singlet state and the spin triplet states, see this Insight.
The Mermin state for photons is ##\frac{1}{\sqrt{2}} \left(\mid VV \rangle + \mid HH \rangle \right)## where ##V## means the there is an outcome (photon detection) behind one of the coaligned polarizers and ##H## means there is no outcome behind one of the co-aligned polarizers. This state obtains due to conservation of angular momentum at the source as represented by momentum exchange along the source collimation (“yes” or “no” longitudinal). Dehlinger and Mitchell created this state by laser inducing spontaneous parametric downconversion in beta barium borate crystals [8], a process that conserves spin angular momentum as represented by the polarization of the emitted photons. At this point we will focus the discussion on the spin single state for total anti-correlation, since everything said of that state can be easily transferred to the Mermin photon state.
Let us investigate what Alice and Bob discover about these entangled states in the various contexts of their measurements (Figure 2). Alice’s detector responds up and down with equal frequency regardless of the orientation ##\alpha## of her SG magnet. This is in agreement with the relativity principle, aka “no preferred reference frame” (NPRF), where different SG magnet orientations relative to the source constitute different “reference frames” in quantum mechanics just as different velocities relative to the source constitute different “reference frames” in special relativity (see this Insight).
Figure 2. Alice and Bob making spin measurements in the xz plane on a pair of spin-entangled particles with their Stern-Gerlach (SG) magnets and detectors.
Bob observes the same regarding his SG magnet orientation ##\beta##. Thus, the source is rotationally invariant in the spatial plane P orthogonal to the source collimation. When Bob and Alice compare their outcomes, they find that their outcomes are perfectly anti-correlated (##ud## and ##du## with equal frequency) when ##\alpha – \beta = \theta = 0## (Figure 3). This is consistent with conservation of angular momentum per classical mechanics between the pair of detection events (again, this fact defines the state). The degree of that anti-correlation diminishes as ##\theta \rightarrow \frac{\pi}{2}## until it is equal to the degree of correlation (##uu## and ##dd##) when their SG magnets are at right angles to each other. In other words, whenever the SG magnets are orthogonal to each other anti-correlated and correlated outcomes occur with equal frequency, i.e., conservation of angular momentum in one direction is independent of the angular momentum changes in any orthogonal direction. Thus, we wouldn’t expect to see more correlation or more anti-correlation based on conservation of angular momentum for transverse results in the plane P when the SG magnets are orthogonal to each other. As we continue to increase the angle ##\theta## beyond ##\frac{\pi}{2}## the anti-correlations continue to diminish until we have totally correlated outcomes when the SG magnets are anti-aligned. This is also consistent with conservation of angular momentum, since the totally correlated results when the SG magnets are anti-aligned represent momentum exchanges in opposite directions in the plane P just as when the SG magnets are aligned, it is now simply the case that what Alice calls up, Bob calls down and vice-versa.
The counterpart for the Mermin photon state is simply that angular momentum conservation is evidenced by ##VV## or ##HH## outcomes for coaligned polarizers. When the polarizers are at right angles you have only ##VH## and ##HV## outcomes, which is still totally consistent with conservation of angular momentum as ‘not ##H##’ implies ##V## and vice-versa [8]. In other words, a polarizer does not have a ‘north-south’ distinction (longitudinal rather than transverse momentum exchange). In particular, having rotated either or both polarizers by ##\pi## one should obtain precisely ##VV## or ##HH## outcomes again.
Nothing is particularly mysterious about the entangled states for electron spin or photon polarization described here so far because we have been thinking as if conservation of angular momentum holds for each experimental trial, as in classical mechanics. Truth is, since Alice and Bob can only measure +1 or -1 (quantum exchange of momentum per NPRF), we can only get conservation of angular momentum in any particular trial when their SG magnets/polarizers are co-aligned. And, we cannot use classical probability theory to account for the conservation of angular momentum on average.
In particular, the probability that Alice and Bob will measure ##uu## or ##dd## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityuu}\end{equation}
And, the probability that Alice and Bob will measure ##ud## or ##du## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityud}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##u##) and -1 (##d##) gives Eq. (\ref{CHSH1}) of
\begin{equation}-\cos(a – b) -\cos(a – b^\prime) -\cos(a^\prime – b) +\cos(a^\prime – b^\prime) \label{CHSHspin}\end{equation}
Choosing ##a = \pi/4##, ##a^\prime = -\pi/4##, ##b = 0##, and ##b^\prime = \pi/2## minimizes Eq. (\ref{CHSHspin}) at ##-2\sqrt{2}## (the Tsirelson bound).
Likewise, for the Mermin photon state we have
\begin{equation}P_{VV} = P_{HH} = \frac{1}{2} \mbox{cos}^2 \left(\alpha – \beta \right) \label{probabilityVV}\end{equation}
and
\begin{equation}P_{VH} = P_{HV} = \frac{1}{2} \mbox{sin}^2 \left(\alpha – \beta \right) \label{probabilityVH}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##V##) and -1 (##H##) gives Eq. (\ref{CHSH1}) of
\begin{equation}\cos2(a – b) +\cos2(a – b^\prime) +\cos2(a^\prime – b) -\cos2(a^\prime – b^\prime) \label{CHSHmermin}\end{equation}
Using ##a = \pi/8##, ##a^\prime = -\pi/8##, ##b = 0##, and ##b^\prime = \pi/4## maximizes Eq. (\ref{CHSHmermin}) at ##2\sqrt{2}## (the Tsirelson bound). So, we have two mysteries.
First, as explained by Mermin [5], suppose you restrict Alice and Bob’s measurement angles ##\alpha## and ##\beta## to three possibilities, setting 1 is ##0^o##, setting two is ##120^o##, and setting three is ##-120^o##. Eq. (\ref{probabilityud}) says the probability of getting opposite results is 1 when ##\alpha = \beta## (1/2 ##ud## and 1/2 ##du##) and 1/4 otherwise (1/8 ##ud## and 1/8 ##du##). Now, if the source emits particles with definite properties that account for their outcomes in the three possible measurement settings, and we have to get total anti-correlation for like settings, then the particles’ so-called “instruction sets” must be opposite for each of the three settings. For example, suppose we have 1(##u##)2(##u##)3(##d##) for Alice and 1(##d##)2(##d##)3(##u##) for Bob. That guarantees the total anti-correlation for like settings, i.e., 11 gives ##ud##, 22 gives ##ud##, and 33 gives ##du##. And, for unlike settings we get anti-correlation in two combinations, i.e., 12 gives ##ud## and 21 gives ##ud##. In fact, for any instruction set with two ##u## and one ##d## we get anti-correlation for unlike settings in two of the six possible unlike combinations (12,13,21,23,31,32). The only other way to make a pair of instruction sets is to have one with all ##u## and the other with all ##d##. In that case, we get anti-correlation for all six unlike combinations. That means the instruction sets necessary to guarantee anti-correlation for like settings lead to an overall anti-correlation greater than 2/6 for unlike settings, which is greater than the quantum probability for anti-correlation in unlike settings of 1/4. This is Mermin’s version of the Bell inequality [9] (fraction of anti-correlated outcomes for unlike settings must be greater than 2/6) and the manner by which it is violated by quantum correlations (1/4 is less than 2/6). Thus, instruction sets (“counterfactual definiteness”) assumed by classical probability theory cannot account for quantum correlations in this case.
The counterpart to this for the CHSH quantity is that classical correlations give a range of -2 to 2 for the CHSH quantity (“CHSH-Bell inequality”). And, as we saw above, the Tsirelson bound violates the CHSH-Bell inequality. Experiments show that the quantum results can be achieved (violating the Bell inequality), ruling out an explanation of these correlated momentum exchanges via instruction sets per classical probability theory.
The second mystery is that even in cases where we don’t violate the Bell inequality, e.g., ##a = b = 0## and ##a^\prime = b^\prime = \pi/2## which give a CHSH value of 0, we still have conservation of angular momentum. Why is that mysterious? Well, it’s not when the SG magnets are co-aligned, since in those cases we always get a +1 outcome and a -1 outcome for a total of zero. But, in trials where ##\alpha – \beta = \theta## does not equal zero, we need either Alice or Bob, at minimum, to measure something less than 1 to conserve angular momentum. For example, if Alice measures +1, then Bob must measure ##-\cos{\theta}## to conserve angular momentum for that trial. But, again, Alice and Bob only measure +1 or -1 (quantum exchange of momentum per NPRF, which uniquely distinguishes the quantum joint distribution from its classical counterpart [10]), so that can’t happen (Figure 4). What does happen? We conserve angular momentum on average in those trials.
It is easy to see how this follows by starting with total angular momentum of zero for binary (quantum) outcomes +1 and -1 (I am suppressing the factor of ##\hbar/2## and I’m referring to the spin singlet state here [11], Figure 3).

Figure 3. Outcomes (yellow dots) in the same reference frame, i.e., outcomes for the same measurement (blue arrows represent SG magnet orientations), for the spin singlet state explicitly conserve angular momentum.
Alice and Bob both measure +1 and -1 results with equal frequency for any SG magnet angle (NPRF) and when their angles are equal they obtain different outcomes giving total angular momentum of zero. The case (a) result is not difficult to understand via conservation of angular momentum, because Alice and Bob’s measured values of spin angular momentum cancel directly when ##\alpha = \beta##, that defines the spin singlet state. But, when Bob’s SG magnet is rotated by ##\alpha – \beta = \theta## relative to Alice’s, the situation is not as clear (Figure 6).
In classical physics, one would say the projection of the angular momentum vector of Alice’s particle ##\vec{S}_A = +1\hat{a}## along ##\hat{b}## is ##\vec{S}_A\cdot\hat{b} = +\cos{(\theta)}## where again ##\theta## is the angle between the unit vectors ##\hat{a}## and ##\hat{b}## (Figure 2). From Alice’s perspective, had Bob measured at the same angle, i.e., ##\beta = \alpha##, he would have found the angular momentum vector of his particle was ##\vec{S}_B = -1\hat{a}##, so that ##\vec{S}_A + \vec{S}_B = \vec{S}_{Total} = 0##. Since he did not measure the angular momentum of his particle at the same angle, he should have obtained a fraction of the length of ##\vec{S}_B##, i.e., ##\vec{S}_B\cdot\hat{b} = -1\hat{a}\cdot\hat{b} = -\cos{(\theta)}## (Figure 4).
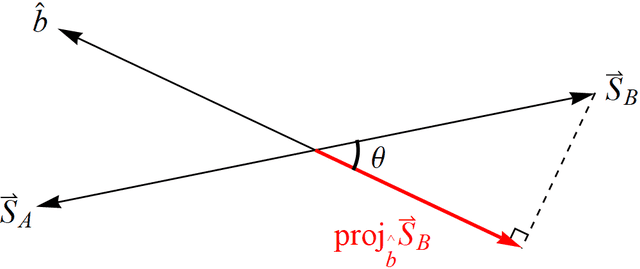
Figure 4. The projection of the angular momentum of Bob’s particle ##\vec{S}_B## along his measurement direction ##\hat{b}##. This does not happen with spin angular momentum due to NPRF.
Of course, Bob only ever obtains +1 or -1 per NPRF, so Bob’s outcomes can only average the required ##-\cos{(\theta)}##. Thus, NPRF dictates
\begin{align*}
P_{uu} + P_{ud} & = \frac {1}{2} \\
P_{ud} + P_{dd} & = \frac {1}{2},
\end{align*}
These equations now allow us to uniquely solve for the joint probabilities
\begin{equation}
P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\theta}{2} \right) \label{QMjointLike}
\end{equation}
and
\begin{equation}
P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\theta}{2} \right) \label{QMjointUnlike}
\end{equation}
\begin{equation}
\overline{BA-} = 2P_{du}(+1) + 2P_{dd}(-1) = \cos (\theta) \label{BA-}
\end{equation}
Using Eqs. (\ref{BA+}) and (\ref{BA-}) in Eq. (\ref{consCorrel}) we obtain
\begin{equation}
\langle \alpha,\beta \rangle = \frac{1}{2}(+1)_A(-\mbox{cos} \left(\theta\right)) + \frac{1}{2}(-1)_A(\mbox{cos} \left(\theta\right)) = -\mbox{cos} \left(\theta\right) \label{consCorrel2}
\end{equation}
which is precisely the correlation function for a spin singlet state found using the joint probabilities per quantum mechanics. To see that we simply use Eqs. (\ref{probabilityuu}) and (\ref{probabilityud}) in Eq. (\ref{average}) to get
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)(-1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(+1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) +\\ &(+1)(+1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(-1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \\ &= -\mbox{cos} \left(\alpha – \beta \right) = -\mbox{cos} \left(\theta \right)
\end{split}
\label{correl}\end{equation}
Thus, “average-only” conservation maps beautifully to our classical expectation (Figures 6 & 7). Since the angle between SG magnets ##\theta## is twice the angle between Hilbert space measurement bases, this result easily generalizes to conservation per NPRF of whatever the measurement outcomes represent when unlike outcomes entail conservation in the symmetry plane [15] (see this Insight on the Bell spin states). However, again, none of the formalism of quantum mechanics is used in obtaining Eq. (\ref{consCorrel2}) or our quantum state Eqs. (\ref{QMjointLike}) & (\ref{QMjointUnlike}). In deriving the quantum correlation function and quantum state in this fashion, we assumed only NPRF.For the Mermin photon state, conservation of angular momentum is established by ##V## (designated by +1) and ##H## (designated by -1) results through a polarizer. When the polarizers are co-aligned Alice and Bob get the same results, half pass and half no pass. Thus, conservation of angular momentum is established by the intensity of the electromagnetic radiation applied to binary outcomes for various polarizer orientations. As with spin angular momentum, this is classical thinking applied to binary outcomes per conservation of angular momentum. Again, grouping Alice’s results into +1 and -1 outcomes we see that she would expect to find ##[\mbox{cos}^2\theta – \mbox{sin}^2\theta]## at ##\theta## for her +1 results and ##[\mbox{sin}^2\theta – \mbox{cos}^2\theta]## for her -1 results. Since Bob measures the same thing as Alice for conservation of angular momentum, those are Bob’s averages when his polarizer deviates from Alice’s by ##\theta##. Therefore, the correlation of results for conservation of angular momentum is given by
\begin{equation}\langle \alpha,\beta \rangle =\frac{(+1_A)(\mbox{cos}^2\theta – \mbox{sin}^2\theta)}{2} + \frac{(-1_A)(\mbox{sin}^2\theta – \mbox{cos}^2\theta)}{2} = \cos{2\theta} \label{merminconserve}\end{equation}
which is precisely the correlation given by quantum mechanics.As before, we need to find ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## so we need four independent conditions. Normalization and ##P_{VH} = P_{HV}## are the same as for the spin case. The correlation function
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)_A(+1)_BP_{VV} + (+1)_A(-1)_BP_{VH} + \\&(-1)_A(+1)_BP_{HV} + (-1)_A(-1)_BP_{HH}\label{correlFn2}
\end{split}
\end{equation}
along with our conservation principle represented by Eq. (\ref{merminconserve}) give
\begin{equation}
P_{VV} – P_{VH} = -\frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
and
\begin{equation}
P_{HV} – P_{HH} = \frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
Solving these four equations for ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## gives precisely Eqs. (\ref{probabilityVV}) & (\ref{probabilityVH}).Notice that since the angle between polarizers ##\alpha – \beta## equals the angle between Hilbert space measurement bases, this result immediately generalizes to conservation per NPRF of whatever the outcomes represent when like outcomes entail conservation in the symmetry plane [15] (again, see this Insight on the Bell spin states).Since the quantum correlations violate the Bell inequality to the Tsirelson bound and satisfy conservation per NPRF while the classical correlations do not violate the Bell inequality, the classical correlations do not satisfy conservation per NPRF. Experiments of course tell us that Nature obeys the quantum correlations and therefore the conservation per NPRF.

Figure 5. A spatiotemporal ensemble of 8 experimental trials for the Bell spin states showing Bob’s outcomes corresponding to Alice‘s ##+1## outcomes when ##\theta = 60^\circ##. Angular momentum is not conserved in any given trial, because there are two different measurements being made, i.e., outcomes are in two different reference frames, but it is conserved on average for all 8 trials (six up outcomes and two down outcomes average to ##\cos{60^\circ}=\frac{1}{2}##). It is impossible for angular momentum to be conserved explicitly in each trial since the measurement outcomes are binary (quantum) with values of ##+1## (up) or ##-1## (down) per no preferred reference frame. The conservation principle at work here assumes Alice and Bob’s measured values of angular momentum are not mere components of some hidden angular momentum with variable magnitude. That is, the measured values of angular momentum are the angular momenta contributing to this conservation.
Figure 6. For the spin singlet state (S = 0). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from –1 (totally down, arrow bottom) to 0 to +1 (totally up, arrow tip). This obtains per conservation of angular momentum on average in accord with no preferred reference frame. Bob can say exactly the same about Alice’s outcomes as she rotates her SG magnets relative to his SG magnets for his +1 outcome. That is, their outcomes can only satisfy conservation of angular momentum on average, because they only measure +1/-1, never a fractional result. Thus, just as with the light postulate of special relativity, we see that no preferred reference frame leads to counterintuitive results (see this Insight).
Figure 7. The situation is similar for the spin triplet states where outcomes agree for the same measurement in the plane containing the conserved angular momentum vector (S = 1). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from +1 (totally up, arrow tip) to 0 to –1 (totally down, arrow bottom). This obtains per conservation of angular momentum on average in the plane containing the S = 1 spin angular momentum in accord with no preferred reference frame. See this Insight for details.
So, while conservation per NPRF sounds like a very reasonable constraint on the distribution of quantum exchange of momentum (+1 or -1, no fractions), we still do not have any causal mechanism to explain the outcomes of any particular trial when the SG magnets/polarizers are not co-aligned (Figure 4). And, as I showed above, we cannot use instruction sets per classical probability theory to account for the Tsirelson bound needed to explain the conservation of angular momentum on average. Thus, while we have a very reasonable constraint on the distribution of entangled quantum exchanges (conservation of angular momentum), that constraint has no compelling dynamical counterpart, i.e., no consensus causal mechanism to explain the outcome of any particular trial when the SG magnets/polarizers are not co-aligned and no counterfactual definiteness to explain why conservation of angular momentum is conserved on average. What we have is a “principle” account of entanglement and the Tsirelson bound (see this Insight). I will return to this point after showing how so-called “superquantum correlations” fail to satisfy this constraint as well.
There are QIT correlations that not only violate the Bell inequality, but also violate the Tsirelson bound. Since these correlations violate the Tsirelson bound, they are called “superquantum correlations.” The reason QIT considers these correlations reasonable (no known reason to reject their possibility) is because they do not violate superluminal communication, i.e., the joint probabilities don’t violate the no-signaling condition
\begin{equation}\begin{split}P(A \mid a\phantom{\prime},b\phantom{\prime}) &= P(A \mid a\phantom{\prime}, b^\prime)\\
P(A \mid a^\prime,b\phantom{\prime}) &= P(A \mid a^\prime, b^\prime)\\
P(B \mid a\phantom{\prime},b\phantom{\prime}) &= P(B \mid a^\prime, b\phantom{\prime})\\
P(B \mid a\phantom{\prime},b^\prime) &= P(B \mid a^\prime, b^\prime )\end{split}\label{nosig}\end{equation}
This means Alice and Bob measure the same outcomes regardless of each other’s settings. If this wasn’t true, Alice and Bob would notice changes in the pattern of their outcomes as the other changed their measurement settings. Since the measurements for each trial can be spacelike separated that would entail superluminal communication.
The Popescu-Rohrlich (PR) joint probabilities
\begin{equation}\begin{split}&P(1,1 \mid a,b) = P(-1,-1 \mid a, b)=\frac{1}{2}\\
&P(1,1 \mid a,b^\prime) = P(-1,-1 \mid a, b^\prime)=\frac{1}{2}\\
&P(1,1 \mid a^\prime,b) = P(-1,-1 \mid a^\prime, b)=\frac{1}{2}\\
&P(1,-1 \mid a^\prime,b^\prime) = P(-1,1 \mid a^\prime, b^\prime)=\frac{1}{2} \end{split}\label{PRcorr}\end{equation}
produce a value of 4 for Eq. (\ref{CHSH1}), the largest of any no-signaling possibilities. Thus, the QIT counterpart to Wheeler’s question, “How Come the Quantum?” is “Why the Tsirelson bound?” [12-14]. In other words, is there any compelling principle that rules out superquantum correlations as conservation of angular momentum ruled out classical correlations? Let us look at Eq. (\ref{PRcorr}) in the context of our spin singlet and Mermin photon states. Again, we will focus the discussion on the spin singlet state and allude to the obvious manner by which the analysis carries over to the Mermin photon state.
The last PR joint probability certainly makes sense if ##a^\prime = b^\prime##, i.e., the total anti-correlation implying conservation of angular momentum, so let us start there. The third PR joint probability makes sense for ##b = \pi + b^\prime##, where we have conservation of angular momentum with Bob having flipped his coordinate directions. Likewise, then, the second PR joint probability makes sense for ##a = \pi + a^\prime##, where we have conservation of angular momentum with Alice having flipped her coordinate directions. All of this is perfectly self consistent with conservation of angular momentum as we described above, since ##a^\prime## and ##b^\prime## are arbitrary per rotational invariance in the plane P. But now, the first PR joint probability is totally at odds with conservation of angular momentum. Both Alice and Bob simply flip their coordinate directions, so we should be right back to the fourth PR joint probability with ##a^\prime \rightarrow a## and ##b^\prime \rightarrow b##. Instead, the first PR joint probability says that we have total correlation (maximal violation of conservation of angular momentum) rather than total anti-correlation per conservation of angular momentum, which violates every other observation. In other words, the set of PR observations violates conservation of angular momentum in a maximal sense. To obtain the corresponding argument for angular momentum conservation per the correlated outcomes of the Mermin photon state, simply start with the first PR joint probability and show the last PR joint probability maximally violates angular momentum conservation.
To find the degree to which superquantum correlations violate our constraint, replace the first PR joint probability with
\begin{equation}\begin{split}&p(1,1 \mid a,b) = C \\
&p(-1,-1 \mid a, b) = D \\
&p(1,-1 \mid a,b) = E \\
&p(-1,1 \mid a, b) = F \\ \end{split} \label{PRcorrMod}\end{equation}
The no-signaling condition Eq. (\ref{nosig}) in conjunction with the second and third PR joint probabilities gives ##C = D## and ##E = F##. That in conjunction with normalization ##C + D + E + F =1## and P(anti-correlation) + P(correlation) = 1 means total anti-correlation (##E = F = 1/2##, ##C = D = 0##) is the conservation of angular momentum per the quantum case while total correlation (##E = F = 0##, ##C = D = 1/2##) is the max violation of conservation of angular momentum per the PR case. To get the corresponding result for the Mermin photon state, simply replace the last PR joint probability in analogous fashion, again with ##\theta = \pi##. In that case, the PR joint probabilities violate conservation of angular momentum with total anti-correlation while the Mermin photon state satisfies conservation of angular momentum with total correlation. Thus, we have a spectrum of superquantum correlations all violating conservation of angular momentum.
So, we see explicitly in this result how quantum mechanics conforms statistically to a conservation principle without need of a ‘causal influence’ or hidden variables acting on a trial-by-trial basis to account for that conservation. That is the essence of a “principle theory.” Indeed, the kinematic structure (Minkowski spacetime) of special relativity and the kinematic structure (qubit Hilbert space) of quantum mechanics both follow from NPRF, so we now know that quantum mechanics is on par with special relativity as a principle theory (again, see this Insight).
Therefore, my answer to QIT’s version of Wheeler’s question is
The Tsirelson bound obtains because of conservation per no preferred reference frame.
Whether or not you consider this apparently simple 4-dimensional (4D) constraint (conservation per NPRF [16,17,18]) to dispel the mystery of entanglement and answer Wheeler’s question depends on whether or not you can accept the fundamentality of a principle explanation via patterns in both space and time (see this Insight). While we have a compelling 4D constraint (who would argue with conservation per NPRF?) for our adynamical explanation, we do not have a compelling dynamical counterpart. That is, we do not have a consensus, causal mechanism to explain outcomes on a trial-by-trial basis when the SG magnets/polarizers are not co-aligned, and we cannot use counterfactual definiteness per classical probability theory to account for the fact that we conserve angular momentum on average. So, perhaps we do not need new physics to rise to Wilczek’s challenge [19].
To me, ascending from the ant’s-eye view to the God’s-eye view of physical reality is the most profound challenge for fundamental physics in the next 100 years.
[Note: “God’s-eye view” simply means the blockworld, block universe, “all-at-once”, or 4D view like that of Minkowski spacetime, there is no religious connotation.] Since special relativity already supports that view, perhaps we should accept that adynamical explanation is fundamental to dynamical explanation, so that not all adynamical explanations have dynamical counterparts [20]. In that case, “we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?” [1]
References
- Wheeler, J.A.: How Come the Quantum?, New Techniques and Ideas in Quantum Measurement Theory 480(1), 304–316 (1986).
- Cirel’son, B.S.: Quantum Generalizations of Bell’s Inequality, Letters in Mathematical Physics 4, 93–100 (1980).
- Landau, L.J.: On the violation of Bell’s inequality in quantum theory, Physics Letters A 120(2), 54–56 (1987).
- Khalfin, L.A., and Tsirelson, B.S.: Quantum/Classical Correspondence in the Light of Bell’s Inequalities, Foundations of Physics 22(7), 879–948 (1992).
- Mermin, N.D.: Bringing home the atomic world: Quantum mysteries for anybody, American Journal of Physics 49(10), 940–943 (1981).
- Bohm, D.: Quantum Theory, Prentice-Hall, New Jersey (1952).
- La Rosa, A.: Introduction to Quantum Mechanics, Chapter 12
- Dehlinger, D., and Mitchell, M.W.: Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory, American Journal of Physics 70(9), 903–910 (2002).
- Bell, J.: On the Einstein-Podolsky-Rosen paradox, Physics 1, 195–200 (1964).
- Garg, A., and Mermin, N.D.: Bell Inequalities with a Range of Violation that Does Not Diminish as the Spin Becomes Arbitrarily Large, Physical Review Letters 49(13), 901–904 (1982).
- Unnikrishnan, C.S.: Correlation functions, Bell’s inequalities and the fundamental conservation laws, Europhysics Letters 69, 489–495 (2005).
- Bub, J.: Bananaworld: Quantum Mechanics for Primates, Oxford University Press, Oxford, UK (2016).
- Bub, J.: Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B, 241–266 (2004).
- Bub, J.: Why the Tsirelson bound?, in The Probable and the Improbable: The Meaning and Role of Probability in Physics, eds. Meir Hemmo and Yemima Ben-Menahem, Springer, Dordrecht, 167–185 (2012).
- Weinberg, S.: The Trouble with Quantum Mechanics (2017).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Kohler, I: Why the Tsirelson Bound? Bub’s Question and Fuchs’ Desideratum, Entropy 21(7), 692 (2019).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Le, T.D.: Answering Mermin’s challenge with conservation per no preferred reference frame, Scientific Reports 10, 15771 (2020).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond Causal Explanation: Einstein’s Principle Not Reichenbach’s, Entropy 23(1), 114 (2021).
- Wilczek, F.: Physics in 100 Years, Physics Today 69(4), 32–39 (2016).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, Oxford University Press, Oxford, UK (2018).
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018).


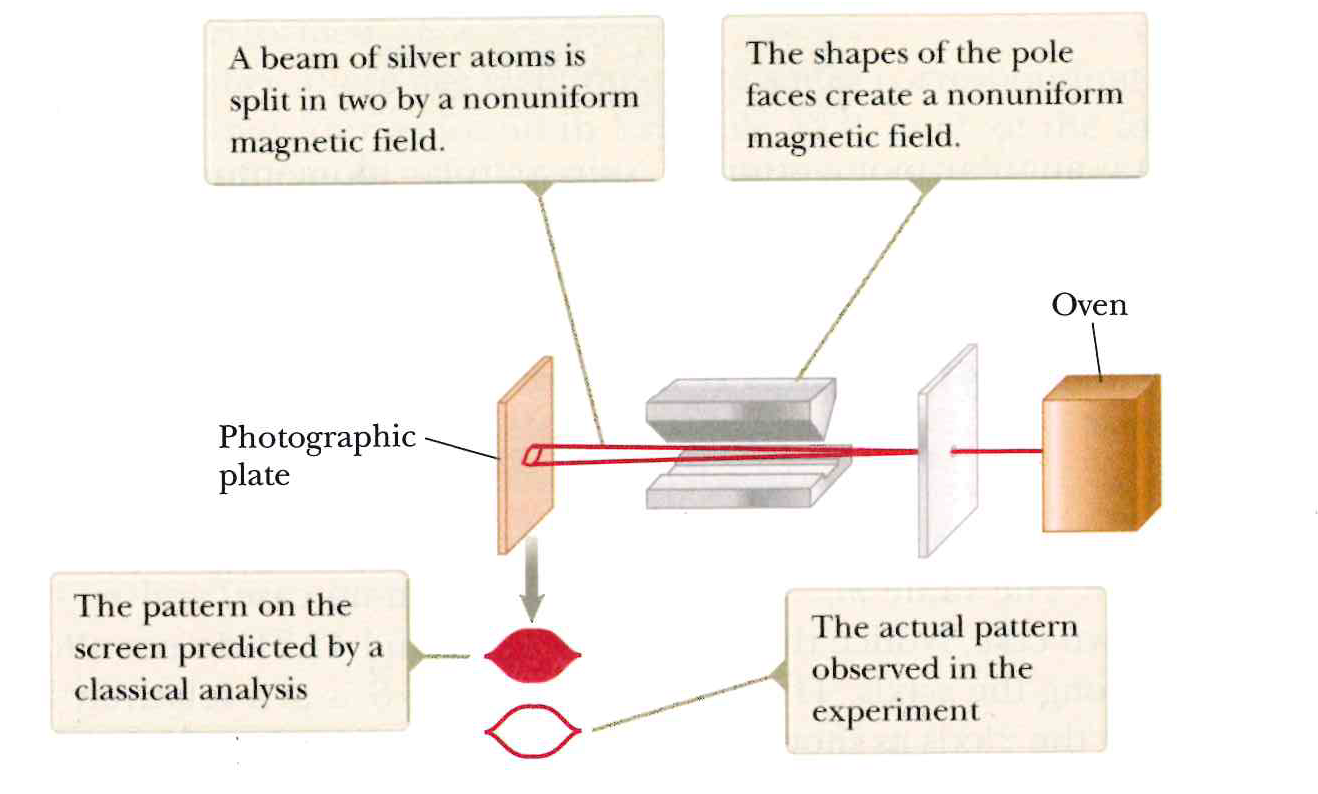 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.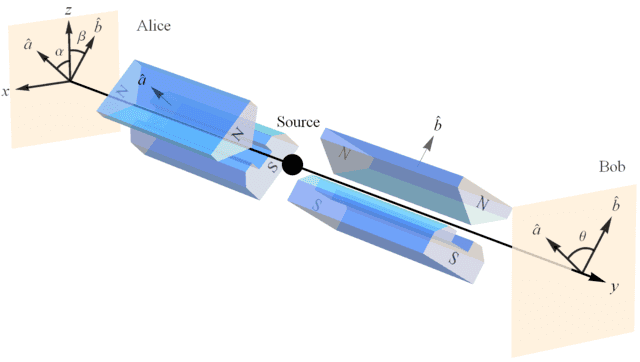








Our quantum-classical model invokes a quantum-classical cut as necessary to use QM (which must be done). Depending on the context, that cut can include screened-off elephants, there is no definitive "size" defining this cut, we don't deviate at all from the practice of QM. It's just a matter of whether or not one is happy with this form of "contextuality" rather than demanding "reductionism" as Weinberg seeks. Again, Nature doesn't demand reductionism and all indications are otherwise, as Weinberg notes. So, do you continue to spend your most precious commodity (your time) seeking "some more satisfactory other theory to which QM is only a good approximation"? Or, do you spend your time looking for new theories of physics, e.g., quantum gravity, via quantum-classical contextuality? Your research direction is determined by your choice for a model of physical reality, precisely as Becker points out.If it were my expertise and if I had some good idea somehow I'd rather try to find a way to formulate a consistent quantum theory of gravitation than tackle some vague philosophical problems with no clear scientific content. I don't believe in the scholastic idea of finding any useful science without a firm confirmation on empirical grounds. That seems to be the reason why we still have no real breakthrough in understanding the most pressing issue in the foundation of physics, i.e., to find a consistent unification of QT (so far relativistic local and microcausal QFTs) and gravity (so far GR, which is a classical relativistic field theory). I think the trouble is that we have not the slightest clue about what effects a quantization of gravity we have to expect since there are no observations hinting at such effects.
There seems to be some misunderstanding! N. P. Landsman writes in "Between classical and quantum" (https://arxiv.org/abs/quant-ph/0506082):
"Describing quantum physics in terms of classical concepts sounds like an impossible and even selfcontradictory task (cf. Heisenberg, 1958). For one, it precludes a completely quantum-mechanical description of the world: ‘However far the phenomena transcend the scope of classical physical explanation, the account of all evidence must be expressed in classical terms.’ But at the same time it precludes a purely classical description of the world, for underneath classical physics one has quantum theory.[SUP]66[/SUP] The fascination of Bohr’s philosophy of quantum mechanics lies precisely in his brilliant resolution of this apparently paradoxical situation.
The first step of this resolution that he and Heisenberg proposed is to divide the system whose description is sought into two parts: one, the object, is to be described quantum-mechanically, whereas the other, the apparatus, is treated as if it were classical. Despite innumerable claims to the contrary in the literature (i.e. to the effect that Bohr held that a separate realm of Nature was intrinsically classical), there is no doubt that both Bohr and Heisenberg believed in the fundamental and universal nature of quantum mechanics, and saw the classical description of the apparatus as a purely epistemological move without any counterpart in ontology, expressing the fact that a given quantum system is being used as a measuring device.[SUP]67[/SUP] For example: ‘The construction and the functioning of all apparatus like diaphragms and shutters, serving to define geometry and timing of the experimental arrangements, or photographic plates used for recording the localization of atomic objects, will depend on properties of materials which are themselves essentially determined by the quantum of action’ (Bohr, 1948), as well as: ‘We are free to make the cut only within a region where the quantum mechanical description of the process concerned is effectively equivalent with the classical description’ (Bohr, 1935).[SUP]68[/SUP]"Between Bohr's (mis)understanding of quantum theory and today are 83 years with tremendous progress not only in the possibility to test quantum theory experimentally but also in the understanding of how the classical behavior of classical systems, including measurement devices, can be understood in terms of many-body quantum theory. The possibility of a local deterministic description of Nature is ruled out with the amazingly accurate measurements of all kinds of Bell tests. The emergence of a "classical world" is of course statistical as is all of many-body physics.
This is completely wrong. There is no quantum reality in Copenhagen.There's no quantum reality in Copenhagen, but in the minimal statistical interpretation there is. It's just excepting the fundamental result of quantum theory that Nature is intrinsically probabilistic and cannot be described with local deterministic models.
In fact, there is no physical decomposition into a classical and a quantum world; at least there's not the slightest empirical evidence for something like this (known also as the "quantum-classical cut" in the infamous Copenhagen class of interpretations; it's the 2nd-most ugly and unnecessary assumption of the adepts of the Copenhagen quantum gibberish; only the idea of a collapse is uglier and more misleading!).There seems to be some misunderstanding! N. P. Landsman writes in "Between classical and quantum" (https://arxiv.org/abs/quant-ph/0506082):
"Describing quantum physics in terms of classical concepts sounds like an impossible and even selfcontradictory task (cf. Heisenberg, 1958). For one, it precludes a completely quantum-mechanical description of the world: ‘However far the phenomena transcend the scope of classical physical explanation, the account of all evidence must be expressed in classical terms.’ But at the same time it precludes a purely classical description of the world, for underneath classical physics one has quantum theory.[SUP]66[/SUP] The fascination of Bohr’s philosophy of quantum mechanics lies precisely in his brilliant resolution of this apparently paradoxical situation.
The first step of this resolution that he and Heisenberg proposed is to divide the system whose description is sought into two parts: one, the object, is to be described quantum-mechanically, whereas the other, the apparatus, is treated as if it were classical. Despite innumerable claims to the contrary in the literature (i.e. to the effect that Bohr held that a separate realm of Nature was intrinsically classical), there is no doubt that both Bohr and Heisenberg believed in the fundamental and universal nature of quantum mechanics, and saw the classical description of the apparatus as a purely epistemological move without any counterpart in ontology, expressing the fact that a given quantum system is being used as a measuring device.[SUP]67[/SUP] For example: ‘The construction and the functioning of all apparatus like diaphragms and shutters, serving to define geometry and timing of the experimental arrangements, or photographic plates used for recording the localization of atomic objects, will depend on properties of materials which are themselves essentially determined by the quantum of action’ (Bohr, 1948), as well as: ‘We are free to make the cut only within a region where the quantum mechanical description of the process concerned is effectively equivalent with the classical description’ (Bohr, 1935).[SUP]68[/SUP]"
Of course, in fact everything known for the past 120 or so years demancs a quantum rather than classical description. Classicality is an approximate description valid for macroscopic observables for many-body systems, derivable from QT. This does, however, not imply that macroscopic systems always necessarily behave "classically".
In fact, there is no physical decomposition into a classical and a quantum world; at least there's not the slightest empirical evidence for something like this (known also as the "quantum-classical cut" in the infamous Copenhagen class of interpretations; it's the 2nd-most ugly and unnecessary assumption of the adepts of the Copenhagen quantum gibberish; only the idea of a collapse is uglier and more misleading!). It is just a matter of preparation techniques to reveal quantum behavior of larger and larger objects. Already buckyballs are pretty large objects consisting of 60 carbon atoms, and they can, appropriately cooled be prepared in a way to get quantum-interference effects in the double-slit experiment. It's also clear that it is very easy already for such "mesoscopic" systems to make them behave "classically" by just not cooling them enough. The thermal e.m. radiation of a few photons is already enough "coupling to the environment" to get enough decoherence to justify a classical description.
Other really macroscopic systems are known to show quantum behavior even before modern QT has been discovered. One historically important example is the specific heat of solids at low temperatures. Famously Einstein and in a refined way Debye early on explained (at least qualitatively) the observed behavior of the specific heat at low temperatures applying the "old quantum theory" to the collective modes of lattice vibrations.This is completely wrong. There is no quantum reality in Copenhagen.
Our quantum-classical model invokes a quantum-classical cut as necessary to use QM (which must be done). Depending on the context, that cut can include screened-off elephants, there is no definitive "size" defining this cut, we don't deviate at all from the practice of QM. It's just a matter of whether or not one is happy with this form of "contextuality" rather than demanding "reductionism" as Weinberg seeks. Again, Nature doesn't demand reductionism and all indications are otherwise, as Weinberg notes. So, do you continue to spend your most precious commodity (your time) seeking "some more satisfactory other theory to which QM is only a good approximation"? Or, do you spend your time looking for new theories of physics, e.g., quantum gravity, via quantum-classical contextuality? Your research direction is determined by your choice for a model of physical reality, precisely as Becker points out.
Of course, in fact everything known for the past 120 or so years demancs a quantum rather than classical description. Classicality is an approximate description valid for macroscopic observables for many-body systems, derivable from QT. This does, however, not imply that macroscopic systems always necessarily behave "classically".
In fact, there is no physical decomposition into a classical and a quantum world; at least there's not the slightest empirical evidence for something like this (known also as the "quantum-classical cut" in the infamous Copenhagen class of interpretations; it's the 2nd-most ugly and unnecessary assumption of the adepts of the Copenhagen quantum gibberish; only the idea of a collapse is uglier and more misleading!). It is just a matter of preparation techniques to reveal quantum behavior of larger and larger objects. Already buckyballs are pretty large objects consisting of 60 carbon atoms, and they can, appropriately cooled be prepared in a way to get quantum-interference effects in the double-slit experiment. It's also clear that it is very easy already for such "mesoscopic" systems to make them behave "classically" by just not cooling them enough. The thermal e.m. radiation of a few photons is already enough "coupling to the environment" to get enough decoherence to justify a classical description.
Other really macroscopic systems are known to show quantum behavior even before modern QT has been discovered. One historically important example is the specific heat of solids at low temperatures. Famously Einstein and in a refined way Debye early on explained (at least qualitatively) the observed behavior of the specific heat at low temperatures applying the "old quantum theory" to the collective modes of lattice vibrations.
ED = environmental decoherence. Here is the explicit quote (p 3 Landau & Lifshitz, 1977) Thus quantum mechanics occupies a very unusual place among physical theories: it contains classical mechanics as a limiting case, yet at the same time it requires this limiting case for its own formulation. In order to construct the QM propagator you use the classical action. QM is built around CM. That's why Weinberg is not happy with it (p 124 Sabine, 2018) You would like to understand macroscopic things like experimental apparatuses and human beings in terms of the underlying theory. You don't want to see them brought in on the level of axioms of the theory. … In my view we ought to take seriously the possibility of finding some more satisfactory other theory to which QM is only a good approximation. … I have tried very hard to develop that more satisfactory other theory without success … It is very hard to do better than QM. So, why not simply work with a quantum-classical model of physical reality? There's nothing in Nature demanding "quantum rather than classical." And we still have a beautiful quantum decomposition of classical systems (as you point out), even if such decompositions require a classical context. We just can't apply that decomposition in toto (as you point out).
We'll put these points back into foundations of physics versions of the paper :-)
That measurement apparati are macroscopic seems to be evident since we need macroscopic bodies to be able to read off the measurement result. I cannot follow your other statements clearly since I've no clue what the acronym ED might mean. Anyway, QM does not need CM to be formulated.The fundamental postulates are independent of CM.
But the "classical environment" can be described as a coarse-grained quantum-many-body system in the sense that you can derive the classical Boltzman transport equation by a gradient expansion or an ##hbar## expansion of the full Kadanoff-Baym equations. There is no necessity for a quantum-classical cut, because the classical behavior of macroscopic systems (in usual everyday states) can be understood from QT via suitable approximations.
In the same sense Newtonian mechanics is valid as an approximation of relativistic mechanics in its range of applicability (slow motions and not too strong gravitational and em. fields).Yes but to get from many quantum systems to a classical system via ED requires a classical environment. ED is an add-on to QM and QM requires CM. We had a nice quote from Landau & Lifshitz saying QM is unique among theories of physics in that it requires its limiting theory (CM). What we have now is a quantum-classical self-consistency with ED and QM and CM. So if you can accept a quantum-classical model of physical reality as we proposed, you’re not going to look for some purely quantum theory underwriting QM. Both Weinberg and Hardy seem to disagree and consequently they spend much time looking for that more fundamental theory. Again your model of physical reality largely determines your approach to physics.
Decoherence requires a classical environment, so it cannot explain classicality as arising from quantum systems, it can only explain how the quantum and classical relate to each other. In the IJQF version of the paper we made an argument for quantum-classical contextuality along those lines, but that's the part of the paper we took out for submission to a physics journal :-)But the "classical environment" can be described as a coarse-grained quantum-many-body system in the sense that you can derive the classical Boltzman transport equation by a gradient expansion or an ##hbar## expansion of the full Kadanoff-Baym equations. There is no necessity for a quantum-classical cut, because the classical behavior of macroscopic systems (in usual everyday states) can be understood from QT via suitable approximations.
In the same sense Newtonian mechanics is valid as an approximation of relativistic mechanics in its range of applicability (slow motions and not too strong gravitational and em. fields).
I really liked this insight, but I am confused about dynamical vs adynamical.
The concept of average (and ensemble) it what is not "real". As far as I understand QM (or even classic statistical mechanics) it is the observer effect.
Is there a formal way to slice a 4D volume (non arbitrary, for all FoR) where this quantity is conserved ?
(keep in mind a am a layman in your response)If you’re a layman and you understood my Insight, give yourself a pat on the back. I wrote that for my undergrad QM students and colleagues on PF.
Apparently, the concept of average is “more real” in QM than the facts for any given trial. That’s the point of the argument. Doing a Lorentz boost to some other FoR (Charlie’s) in motion wrt Alice and Bob would not obscure this result because Charlie would still see the spacelike correlations.
I really liked this insight, but I am confused about dynamical vs adynamical.
Whether or not you consider this apparently simple 4-dimensional (4D) constraint (conservation of angular momentum on average)The concept of average (and ensemble) it what is not "real". As far as I understand QM (or even classic statistical mechanics) it is the observer effect.
Is there a formal way to slice a 4D volume (non arbitrary, for all FoR) where this quantity is conserved ?
(keep in mind a am a layman in your response)
Decoherence requires a classical environment, so it cannot explain classicality as arising from quantum systems, it can only explain how the quantum and classical relate to each other. In the IJQF version of the paper we made an argument for quantum-classical contextuality along those lines, but that's the part of the paper we took out for submission to a physics journal :-)
Again, this is where your model of physical reality bears significantly on how you do physics. If your model of physical reality is quantum-classical, i.e., both are equally fundamental, then you don't spend any of your research time trying to better quantum mechanics. Both Hardy and Weinberg have spent years trying to do that without success. As Weinberg discovered, "It is very hard to do better than quantum mechanics'' (p 124 of Sabine's book). Hardy tried to find information-theoretic postulates that would uniquely specify QM over classical probability theory and superquantum correlations. He writes, "Either there do exist higher theories in this hierarchy or there do not. For many years I tried to find such theories, and I tried to prove that such theories do not exist. I also tried to find other reasonable axioms that rule out higher theories in this hierarchy" (p 3 of https://arxiv.org/pdf/1303.1538.pdf). What he ended up with are five postulates satisfied by both classical and quantum probability theories. If Hardy's model of physical reality were quantum-classical instead of "quantum rather than classical," he might stop with this last result.
Well, this I can agree with. One should always be open-minded. What I disagree with is the claim that philsophy is of any help to solve physics problems. As you can well see from the quote of Sabine's book, Weinberg doesn't argue philosophically but physically. On the other hand, is this really a problem? There are effective descriptions of decoherence as approximations of QT. Usually this goes via influence-functional methods of quantum-kinetic theory, resulting in master equations for open quantum systems. I find this already a pretty satisfactory explanation for the "classicality" of behavior of macroscopic objects, including measurement devices in the sense of the decoherence program.
There's of course one point, which however is again pretty metaphysical: What's the meaning of the quantum state of the entire universe. Is the entire universe an open system as well? This seems to be a pretty disturbing idea since the universe is, by definition, just everything. So what makes the universe open, if it includes everything? On the other hand, according to standard cosmology (particularly with inflation) we can only observe a tiny bit of the entire universe. So can we interpret the observable part of the universe, which is the only thing that can be described by physics as we usually define it since unobservables are not subject of any serious physics, as an open system? But then there should be interactions of the observable part with the "rest", but that's impossible because by definition the rest is beyond some horizon, i.e., the parts of the observable universe cannot interact with the "rest". If you have such a comprehensive view, I can admit that there is a fundamental problem with the interpretation of quantum theory, but as my just given examples show, it seems as well not so easy to be solved within the scientific method, because it may concern principally unobservable entities, and thus are no longer subject to the scientific realm of human knowledge. Maybe this teaches us that our objective knowledge is in principle always incomplete. Well, the natural sciences teaches us humility. Starting from being the center of the universe (an idea of philosophers by the way ;-)), we've become a humble little accident in a totally unimportant little galaxy at a place that is in no way distinguished from any other place in the universe :-)).
Weinberg seems to favor the "ant's-eye view" per Wilczek. On p 147 in The Geometric Analogy of Gravitation and Cosmology he writes At one time it was even hoped that the rest of physics could be brought into a geometry formulation, but this hope has met disappointment, and the geometric interpretation of the theory of gravitation has dwindled to a mere analogy … it simply doesn't matter whether we ascribe these predictions to the physical effect of gravitational fields on the motion of planets and photons or to a curvature of space and time. (The reader should be warned that these views are heterodox and would meet with objections from many general relativists.) His view, as he makes clear elsewhere, is the action of gravitational fields on matter not the 4D view of spacetime curvature. That dynamical view of physical reality then leads him to believe QM is not complete. Here is a Weinberg quote in Sabine's book (p. 126-7) You can very well understand quantum mechanics in terms of an interaction of the system you're studying with an external environment which includes an observer, but this involves a quantum mechanical system interacting with a macroscopic system that produces the decoherence between different branches of the initial wave function. And where does that come from? That should be described also quantum mechanically. And, strictly speaking, within quantum mechanics itself there is no decoherence.This is a nonstarter if you accept the 4D view (Wilczek's "God's-eye view") of QM as I explain in the Insight. Your model of physical reality will greatly influence how you do physics. That's why, as Becker argues, it's important for physicists to reflect seriously on their models. They don't need to make a career of studying different models, as in foundations, but they should all be aware of existing or possible alternative models within their own fields.
The weirdness is trivially resolved if you accept the QM predictions, which we know give CM via averages. That's what most physicists do, i.e., most physicists don't bother with foundations of QM. This attitude is famously called "shut up and calculate" by Mermin. As argued by Becker, physicists do require physical models to do physics (he has some nice examples in his book) and these models are what allow physicists to create new approaches to theory and experiment. Einstein thought QM was incomplete precisely because his model of physical reality would not accommodate QM predictions for entangled states. Bell's inequalities were derived precisely in response to Einstein's model of physical reality. In Sabine's new book, even Weinberg admits to looking for a theory underwriting QM because it violates his model of physical reality (that's not how he worded it of course).It's of course true that you need intuitive pictures about physics to "create" (or rather "discover") new theoretical models, but Einstein is a prime example for the danger of being trapped in philosophical prejudices.
Of course, in some sense the minimal statistical interpretation indeed is indeed a kind of nicer expression for "shutup and calculate". The question is whether you can expect more from a natural science than just this: You have a model (or even theory) which allows you to predict the outcome of observations, measurements, and experiments and than compare these expectations with the observations. If these expectations agree with the data, it's fine for the model, otherwise you have to think harder about what's wrong with the model and find a new one. This is indeed a creative act, and you need intuitive pictures to get the (finally) the right idea how to describe the phenomena with existing (which is almost always the case) models/theories or you have to find a new one (this occured only two times after Newton, i.e., with the discovery of relativity around 1905 and of quantum theory in 1925).
I know that Weinberg thinks there is something unsolved with the foundations of quantum theory from his textbook on quantum mechanics (as always among the best textbooks on the subject). Although for me Weinberg is a role model for how to do theoretical physics (with a strict "no-nonsense approach" and with a clear mathematical exposition of all the papers and textbooks by him I'm aware of), this I do not understand, since there's no contradiction whatsoever with quantum theory and its application to real-world observations. So what should be incomplete in its applications?
I've not yet read Hossenfelders new book. The title "lost in math" already appalls me, since my view on theoretical physics is the opposite (I'd rather say "lost without math" ;-)), but I think she has indeed a point in saying that maybe we have to widen our view to new (mathematical) methodology beyond the symmetry paradigm, which was indeed the right paradigm for 20th-century physics in creating quantum theory (for me there's no convincing way to formulate quantum theory without symmetry principles and Nother's works on symmetries and conservation laws), relativity, and the Standard Models of elementary particle physics and cosmology, but it may well be that we need new methods to find a unified theory of QT and GR. She is also right in saying that it is hard to conceive whether we have a chance without new empirical findings clearly contradicting one of these fundamental theories (or rather our best approximation of the maybe and hopefully existing but yet undiscovered more comprehensive theory).
Towards Becker's book, I've a mixed feeling. On the one hand I find it overdue to get Bohr, Heisenberg, et al from their pedestal. The true interpretational problem is due to the unjustified predominance of the Copenhagen flavor of interpretations, and Bohr's writings on the subject doing more harm than good, because they are usually not well formulated and too vague and too qualitative ("lost without math"! indeed) to be not subject to speculations about their meaning. That said, Heisenberg is even worse! On the other hand, I cannot agree with Becker's enthusiasm for the de Broglie-Bohm approach since there's to my knowledge no convincing formulation of relativistic QFT within this approach. Any interpretation must be an interpretation of all of the working QTs, applied to real-world phenomena, and this includes relativistic local QFT although it's still not a mathematically strictly defined theory.
What we're saying in our paper and book (and how I close my Insight) is that there is a model of physical reality (not simply "shut up and calculate" aka "instrumentalism") for which QM makes sense and is compatible with relativity. In this Insight, we see that the QM correlations follow from conservation of angular momentum for the quantum exchange of momentum as required for no preferred reference frame. That's compelling, but provides no 'causal influence' or hidden variables to account dynamically for the outcomes on a trial-by-trial basis. The constraint here only holds over space AND time, it's truly 4D, and it has no compelling dynamical counterpart. What we argue in our book (and in my blockworld Insight series) is that 4D constraints are fundamental, not dynamical laws. Most people disagree strongly with this (consider Fermat's Principle of Least Time versus Snell's Law, for example, which really explains the light ray's trajectory?). However, in case after case, we see that mysteries arise in physics because we demand dynamical explanation and all such mysteries disappear when we accept the explanation via 4D constraints. This is just one of many such examples.Well, I've to read the Insight article again. So far I couldn't get the content of the whole approach :-(. I also do not understand, what philosophers and philosophy-attached physicists mean, when they talk about "reality". For me QT is the best description of reality we have, and the only thing that's incomplete with it is the lack of a consistent quantum description of gravity. For me there's no interpretational issue at all, and I don't think that looking for classical/deterministic non-local descriptions have a chance to lead to anything, because a non-local theory is hard to formulate within relativistic physics. One historical failure is Feynman's and Wheeler's attempt to formulate an action at a distance (non-local) theory for interacting systems of charged particles. Although this "absorber theory" seems to work to some extent on a classical level, there was (so far) nobody able to build a quantum formulation of it.
So, this Insight really vindicates the shut-up-and-calculate attitude by providing a model of physical reality in which QM doesn't need to be 'fixed' or underwritten (anymore so than we already have with QFT anyway). QM is in beautiful accord with a truly 4D reality constrained in 4D fashion in such a way as to guarantee dynamical experience per CM.
I spent 24 years trying to figure out Mermin's "quantum mysteries for anybody." I finally feel as though I have the answer (a model of physical reality in which QM entanglement is in perfect accord with CM and SR). The invariant manner by which Mermin's "mysterious" QM correlations follow from conservation principles and lead to CM honestly makes me say, "how could I have been so stupid for so long?"QM entanglement is in perfect accord with SR and with none local classical model. So there must be a non-local aspect in what you call "classical mechanics", but as I said, I better make another attempt to understand your Insight article.
As in all cases of apparent "quantum weirdness" I know, the minimal statistical interpretation resolves the weirdness. The only weirdness remaining is due to our classically trained prejudices about the behavior of objects, but these prejudices are due to our everyday experience with very much coarse-grained macroscopic observables, which are in fact averaging over many microscopic degrees of freedom, which leads to an apparent classical behavior, but in fact it's just due to the sufficiency of coarse-grained macroscopic observables to describe macroscopic systems. On these macroscopic scales all the quantum fluctuations (in the sense of statistical processes) are irrelevant to the accuracy of our everyday observations.The weirdness is trivially resolved if you accept the QM predictions, which we know give CM via averages. That's what most physicists do, i.e., most physicists don't bother with foundations of QM. This attitude is famously called "shut up and calculate" by Mermin. As argued by Becker, physicists do require physical models to do physics (he has some nice examples in his book) and these models are what allow physicists to create new approaches to theory and experiment. Einstein thought QM was incomplete precisely because his model of physical reality would not accommodate QM predictions for entangled states. Bell's inequalities were derived precisely in response to Einstein's model of physical reality. In Sabine's new book, even Weinberg admits to looking for a theory underwriting QM because it violates his model of physical reality (that's not how he worded it of course).
What we're saying in our paper and book (and how I close my Insight) is that there is a model of physical reality (not simply "shut up and calculate" aka "instrumentalism") for which QM makes sense and is compatible with relativity. In this Insight, we see that the QM correlations follow from conservation of angular momentum for the quantum exchange of momentum as required for no preferred reference frame. That's compelling, but provides no 'causal influence' or hidden variables to account dynamically for the outcomes on a trial-by-trial basis. The constraint here only holds over space AND time, it's truly 4D, and it has no compelling dynamical counterpart. What we argue in our book (and in my blockworld Insight series) is that 4D constraints are fundamental, not dynamical laws. Most people disagree strongly with this (consider Fermat's Principle of Least Time versus Snell's Law, for example, which really explains the light ray's trajectory?). However, in case after case, we see that mysteries arise in physics because we demand dynamical explanation and all such mysteries disappear when we accept the explanation via 4D constraints. This is just one of many such examples.
So, this Insight really vindicates the shut-up-and-calculate attitude by providing a model of physical reality in which QM doesn't need to be 'fixed' or underwritten (anymore so than we already have with QFT anyway). QM is in beautiful accord with a truly 4D reality constrained in 4D fashion in such a way as to guarantee dynamical experience per CM.
I spent 24 years trying to figure out Mermin's "quantum mysteries for anybody." I finally feel as though I have the answer (a model of physical reality in which QM entanglement is in perfect accord with CM and SR). The invariant manner by which Mermin's "mysterious" QM correlations follow from conservation principles and lead to CM honestly makes me say, "how could I have been so stupid for so long?"
Yes, but you'll get zero by measuring the angular momentum in any direction. I guess, I now get the problem you want to discuss. Of course, you can for each single decay only measure the angular momentum in one direction, not in three linearly independent ones since angular-momentum components at different directions are not compatible to each other.Right, the classical picture would have definite values for ##vec{L_A}## and ##vec{L_B}## for each of Alice and Bob's particles, respectively. ##vec{L_A}## and ##vec{L_B}## would have the same magnitude L and be anti-aligned along some direction in space (call that direction ##vec{d}##). When Alice and Bob make measurements of ##vec{L_A}## and ##vec{L_B}## along ##vec{A}## and ##vec{B}##, respectively, they will get fractions of L correlated per conservation of angular momentum. In the quantum case, they both always measure L in every direction in such a way that Alice(Bob) can claim her(his) measurements were always along ##vec{d}## and Bob's(Alice's) "incorrect" measurements averaged to the correct value. So, for QM there is no preferred ##vec{d}## for this conserved vector quantity.
Yes, but you'll get zero by measuring the angular momentum in any direction. I guess, I now get the problem you want to discuss. Of course, you can for each single decay only measure the angular momentum in one direction, not in three linearly independent ones since angular-momentum components at different directions are not compatible to each other.
Now all the quibbles with this gets resolved, when you take the minimal statistical interpretation seriously and accept that the meaning of quantum states are probabilities for the outcome of measurements according to Born's rule and nothing else (and you cannot know more, if QT is correct, which I assume due to the lack of any contradictions of experience to the predictions of QT): To verify the probabilistic predictions of quantum theory you have to consider an ensemble of very many decaying particles and measure the angular-momentum components in three linearly independent on a sufficiently large subensemble for each direction since you can only measure one component for each single event. The prediction of QT is a 1:1 correlation between the outcomes of A's and B's measurement of the spin components of the decay particles in the same direction, and this holds true for any direction, and this is in full accordance with angular-momentum conservation. Of course the outcome of these measurements is completely random, but the correlation holds strictly true (with 100% probability).
As in all cases of apparent "quantum weirdness" I know, the minimal statistical interpretation resolves the weirdness. The only weirdness remaining is due to our classically trained prejudices about the behavior of objects, but these prejudices are due to our everyday experience with very much coarse-grained macroscopic observables, which are in fact averaging over many microscopic degrees of freedom, which leads to an apparent classical behavior, but in fact it's just due to the sufficiency of coarse-grained macroscopic observables to describe macroscopic systems. On these macroscopic scales all the quantum fluctuations (in the sense of statistical processes) are irrelevant to the accuracy of our everyday observations.
I said something that may have contributed to vanhees71’s confusion. I said these states have no preferred direction for a conserved vector quantity. Well since the conserved vector is null that’s a stupid thing to say. I should have said Alice and Bob are always measuring non-zero L that always cancel when co-aligned. So when not co-aligned we expect fractional results from either at minimum. Instead these two vectors are always the same length such that either cancels the other on average. That’s the sense in which we have conservation of a vector quantity with no preferred direction.
What do you mean by this?
In classical theory you also have conservation of angular momentum for any closed system. If you take some bomb sitting somewhere at rest, and it's exploding without any outside influence (e.g., by some time fuse within the bomb itself triggering the explosion, i.e., without any external transfer of angular momentum) the total angular momentum of the pieces flying apart is still 0. This is qualitatively not different from the quantum-mechanical example of a decaying (pseudo-)scalar particle into two spin-1/2 particles (e.g., ##pi^+ rightarrow mu^+ + nu_{mu}##). The total angular momentum in the rest frame of the pion (center-mass frame of the muon and muon-neutrino) is 0.
I don't understand the statement about the measurement on a conserved vector quantity.For the bomb, you add up the momenta of all the pieces and get zero. For the decay of a neutral pi meson, the electron and positron will only give zero total spin if you measure each piece along the same axis.
Ok, then I misunderstood the purpose of this entire discussion. I thought it was about quantum mechanics.Well, it is in the sense that the exercise leads to the same conditional probabilities as QM.
What do you mean by this?
In classical theory you also have conservation of angular momentum for any closed system. If you take some bomb sitting somewhere at rest, and it's exploding without any outside influence (e.g., by some time fuse within the bomb itself triggering the explosion, i.e., without any external transfer of angular momentum) the total angular momentum of the pieces flying apart is still 0. This is qualitatively not different from the quantum-mechanical example of a decaying (pseudo-)scalar particle into two spin-1/2 particles (e.g., ##pi^+ rightarrow mu^+ + nu_{mu}##). The total angular momentum in the rest frame of the pion (center-mass frame of the muon and muon-neutrino) is 0.
I don't understand the statement about the measurement on a conserved vector quantity.
Perhaps I should read more carefully your insights article, but this line of arguments is very strange to me. In classical Newtonian as well as special relativistic physics the total angular momentum of a closed system is conserved by construction since it follows from the isotropy of both Galilei-Newton as well we Einstein-Minkowski spacetime. In classical statistical mechanics this still holds strictly true too. So I don't get the point of this argument.
There's also no preferred reference frame in both classical and quantum theory by construction. Again it's a mathematical consequenz of Galilei or Poincare invariance of the physical laws. Indeed, the geometrical approach in a modern sense is a great element of beauty, and I don't see any necessity to destroy this beauty!But, in quantum mechanics, we can have conservation of a directional quantity with no preferred direction! That doesn't even make sense classically where you're only going to measure a fraction of the magnitude of the conserved vector quantity when you measure in another direction. That's pretty cool.
But the connection with quantum mechanics is that the conditional probabilities–##P_1## = the conditional probability that Bob measures spin-up along ##vec{B}## given that Alice measures spin-up along ##vec{A}##, and ##P_2## = the probability that Bob measures spin-down–are the same as the quantum prediction for EPR.
I don't understand what you find confusing. Computing the quantum prediction of relative probabilities, or the statement of the problem?Ok, then I misunderstood the purpose of this entire discussion. I thought it was about quantum mechanics. I don't see any clear classical-statistical physics picture of the quite complicated probability-theory exercise either. Still puzzled…
The other thing I learned from these examples is the apparent importance of no preferred reference frame in Nature. The relativity principle, the light postulate, and now the direction-invariant manner by which QM gives rise to conservation of L all speak to the fundamental importance of no preferred reference frame. I've been studying physics for almost 40 years and I'm still discovering elements of its beauty :-)Perhaps I should read more carefully your insights article, but this line of arguments is very strange to me. In classical Newtonian as well as special relativistic physics the total angular momentum of a closed system is conserved by construction since it follows from the isotropy of both Galilei-Newton as well we Einstein-Minkowski spacetime. In classical statistical mechanics this still holds strictly true too. So I don't get the point of this argument.
There's also no preferred reference frame in both classical and quantum theory by construction. Again it's a mathematical consequenz of Galilei or Poincare invariance of the physical laws. Indeed, the geometrical approach in a modern sense is a great element of beauty, and I don't see any necessity to destroy this beauty!
Let me also point out that these calculations are just an example of what we already know about QM. We know entangled states are created from conservation principles and that QM states reproduce CM via expectation values, i.e., on average. So, of course, this result has to follow. I thought it was interesting to see exactly what the general idea (QM gives CM on average) means for these states, but not the least bit surprising. That was Unnikrishnan's attitude in the paper referenced in my Insight — he asked (polemically) why anyone would even bother to check for violations of the Bell inequality. Why would anyone expect classical probability to hold when classical probability would violate conservation of L? Given there are quantum exchanges of momentum, classical probability theory cannot possibly provide for conservation of L, it just cannot hold on a trial-by-trial basis for quantum exchange of momentum.
So, that the Tsirelson bound (extent to which the Bell inequality is violated by QM) follows from the conservation of L for the quantum exchange of momentum is merely showing us an implication of QM –> CM on average when the fundamental exchanges of momentum are quantized. Again, I thought it was cool to see exactly what that means for the spin singlet state per Unnikrishnan and then figuring out what it means for the Mermin photon state myself. These examples really clarified the relationship between QM and CM for me by providing a more physical basis for what I had already written in our book.
And, that relationship provides a beautifully self-consistent model of objective reality (without instrumentalism) as long as you don't require a dynamical model. This example does absolutely nothing to help those stuck in the "ant's-eye view." That's the point of our book and that's the point of this Insight (which is why it's linked to my BW series).
I thought I was pretty clear, but I can try again. Forget quantum mechanics for a second, and let's consider the following purely mathematical problem:
Question: Find ##P_1## and ##P_2##
So it's a purely mathematical problem. The claim being made is that 1-8 allows you to deduce the answer to the question. You cannot bring up quantum mechanics to answer the question, because that's not one of the assumptions 1-8.
But the connection with quantum mechanics is that the conditional probabilities–##P_1## = the conditional probability that Bob measures spin-up along ##vec{B}## given that Alice measures spin-up along ##vec{A}##, and ##P_2## = the probability that Bob measures spin-down–are the same as the quantum prediction for EPR.
I don't understand what you find confusing. Computing the quantum prediction of relative probabilities, or the statement of the problem?One suggested addition—items 6-8 are from Alice’s perspective. Changing to Bob’s perspective you would be dotting along ##vec{A}## in 8. Either way gives the QM result.
I don't understand what you find confusing. Computing the quantum prediction of relative probabilities, or the statement of the problem?The third possibility, which I also find confusing, is exactly what the significance of the argument is.
It's again not clear to me what you want to calculate.I thought I was pretty clear, but I can try again. Forget quantum mechanics for a second, and let's consider the following purely mathematical problem:
Question: Find ##P_1## and ##P_2##
So it's a purely mathematical problem. The claim being made is that 1-8 allows you to deduce the answer to the question. You cannot bring up quantum mechanics to answer the question, because that's not one of the assumptions 1-8.
But the connection with quantum mechanics is that the conditional probabilities–##P_1## = the conditional probability that Bob measures spin-up along ##vec{B}## given that Alice measures spin-up along ##vec{A}##, and ##P_2## = the probability that Bob measures spin-down–are the same as the quantum prediction for EPR.
I don't understand what you find confusing. Computing the quantum prediction of relative probabilities, or the statement of the problem?
Thanks for the warning. In general, philosophy on quantum theory rather confuses the reader than to help him or her. Maybe your book is an exception. Nevertheless the word philosophy in connection with quantum theory (or even physics in general) should be read as a caveat sign ;-)).There are philosophers who are interested in foundations of physics (FoP) and our book was written for them as well as physicists interested in FoP. As a typical physicist, I tend to make unarticulated assumptions and the philosophers are good at identifying those. My interest in FoP is based on my desire for a model of objective reality for all of physics. See Becker's book for the value in this.
It's again not clear to me what you want to calculate. The joint probability that A finds ##sigma_A=pm 1/2## and B find ##sigma_B=pm 1/2## is, of course
$$P(sigma_A,sigma_B) =|langle sigma_A | otimes langle sigma_B |Psi rangle|^2.$$
Here ##|sigma_A rangle## and ##|sigma_B rangle## are the eigenvalues of the operators
$$hat{sigma}_{A}=vec{A} cdot hat{vec{sigma}}, quad hat{sigma}_{A}=vec{A} cdot hat{vec{sigma}}.$$
I'm to lazy to explicitly figure this out, but I still don't see the point of the exercise :-(.
Yes, but the spin components in non-collinear directions need not to cancel each other. Why should they?That was what I asking RUTA for clarification about.
The sense in which there is cancellation on the average is this:
Among those events where Alice measures spin-up along direction ##vec{A}##, the expectation for
##(vec{S}_A + vec{S}_B) cdot vec{B}## = 0
(where ##vec{S}_A = + frac{1}{2} vec{A}## and ##vec{S}_B = pm frac{1}{2} vec{B}##)
Yes, but the spin components in non-collinear directions need not to cancel each other. Why should they?
That's a different question, which is not describing the statistics you expect from quantum theory as detailed above!I'm not sure what you mean. Both the heuristic argument (not original with me; I was paraphrasing the Insights article) and the quantum theory make the same predictions: If Alice measures her particle's spin along axis ##vec{A}## and Bob measures his particle's spin along axis ##vec{B}##, then the conditional probabilities are:
(where ##theta## is the angle between ##vec{A}## and ##vec{B}##).
Be forewarned about our book — as a mathematician, you'll want to avoid the philosophical threads. The main thread is probably already too philosophical for you :-)Thanks for the warning. In general, philosophy on quantum theory rather confuses the reader than to help him or her. Maybe your book is an exception. Nevertheless the word philosophy in connection with quantum theory (or even physics in general) should be read as a caveat sign ;-)).
The issue was not to derive the quantum probabilities from quantum mechanics, but to see if those probabilities can be derived from the assumptions that:
That's a different question, which is not describing the statistics you expect from quantum theory as detailed above!
The issue was not to derive the quantum probabilities from quantum mechanics, but to see if those probabilities can be derived from the assumptions that:
This whole approach is very new to me. I am very interested in QM foundations, but have been taking a back seat and listening, rather than participating until I feel more comfortable commenting.
Thanks
Bill
Be forewarned about our book — as a mathematician, you'll want to avoid the philosophical threads. The main thread is probably already too philosophical for you :-)Don't worry – I sort of figured that out with its emphasis on the Blockworld which I am not a fan of. But as I often say – my views mean jack shite – I am sure it will contain interesting insights. Every interpretation of QM I have read, transnational, MW, BM etc etc have helped me in understanding the formalism better. My personal views are pretty well known, and are virtually identical to Vanhees, but to hold any view you must subject it to what other views say.
Thanks
Bill
I'm not sure, whether I understand your problem. This is an example for the fact that a single-particle quantity (like single-particle spin) in a many-body system can be determined for the system as a whole (here the total angular momentum) while the single-particle quantities are indetermined. That's an implication of entanglement.
In the here discussed case you have a total angular momentum 0 state of a two-particle system of spin-1/2 particles, i.e., the two-particle spin state is
$$|Psi rangle=frac{1}{sqrt{2}} (|1/2,-1/2 rangle – |-1/2,1/2 rangle).$$The issue was not to derive the quantum probabilities from quantum mechanics, but to see if those probabilities can be derived from the assumptions that:
I'm trying to get an intuitive understanding of the way that EPR probabilities (for anti-correlated spin-1/2 particles) are in some sense the closest we can get to the criteria:
If Alice measures her particle's spin along axis ##A## and Bob measures his particle's spin along axis ##B##, then it is impossible to satisfy both criteria, because unless ##A## and ##B## are aligned, none of the following combinations adds up to zero:
What the quantum probabilities do instead is the following:
This uniquely determines the probabilities ##P_1## and ##P_2##:
The latter equation becomes:
##frac{1}{2} (P_1 (cos(theta) + 1) + P_2 (cos(theta) – 1)) = 0## (where ##theta## is the angle between ##A## and ##B##)
These equations have the unique solution: ##P_1 = frac{1}{2} (1-cos(theta)) = sin^2(frac{theta}{2})##, ##P_2 = frac{1}{2} (1+cos(theta)) = cos^2(frac{theta}{2})##
Those are the quantum probabilities for anti-correlated spin-1/2 particles.
That's sort of interesting, but my understanding of the motivation is a little muddled. I understand that you can't have perfect cancellation if the axes ##vec{A}## and ##vec{B}## are not aligned. But why ask for cancellation (on the average) along axis ##vec{B}##?I'm not sure, whether I understand your problem. This is an example for the fact that a single-particle quantity (like single-particle spin) in a many-body system can be determined for the system as a whole (here the total angular momentum) while the single-particle quantities are indetermined. That's an implication of entanglement.
In the here discussed case you have a total angular momentum 0 state of a two-particle system of spin-1/2 particles, i.e., the two-particle spin state is
$$|Psi rangle=frac{1}{sqrt{2}} (|1/2,-1/2 rangle – |-1/2,1/2 rangle).$$
That's obviously a simultaneous eigenstate of ##|hat{vec{S}}^2 rangle## and ##|hat{S}_z rangle## to the eigenvalues ##S=0##, ##sigma_z=0##. Here
$$hat{vec{S}}=hat{vec{s}} otimes hat{1} + hat{1} otimes hat{vec{s}}.$$
Note that the ##S=0## state is very special, because in this case all three components of ##vec{S}## are determined although these operators do not commute.
Nevertheless the single-particle spins are maximally undetermined, i.e., there probabilities are given by the Statistical operator
$$hat{rho}_A=mathrm{Tr}_B |Psi rangle langle Psi|=frac{1}{2} hat{1}$$
and
$$hat{rho}_B=mathrm{Tr}_A |Psi rangle langle Psi|=frac{1}{2} hat{1}.$$
Now measuring the angular momentum component at particles A and B in different directions you get the probabilities you quote, and that's all you know about the outcome of measurements of the single-particle angular momenta. Of course, the measured outcomes do not add up to 0. Why should they? Even in classical physics it doesn't make too much sense to add components of vectors with respect to basis vectors in different directions. Of course, if you measure the angular-momentum components for both particles wrt. the same direction, then they must add up to 0 due to the preparation of the two-body system in the ##S=0## state. As explained above here you have the special case of a preparation of all three angular-momentum components to have the determined value 0. This is special, because that's possible only for the ##S=0## state and is due to the complete rotational symmetry (isotrophy) of this one special state. So you can have sometimes common eigenvectors for incompatible observables, and that's the most common example for this fact.
I don't see any further specialty in this example, despite the fact that it's the most simple example to explain entanglement, Bell's inequality and all such unusual quantum correlations without a classical counterpart. It's only a problem, if you don't accept the quite abstract mathematical formulation of quantum theory and its minimal probabilistic interpretation in terms of Born's rule. Due to our persistent intuition from our experience with classically behaving (quantum) objects (aka many-many-many-…-body systems) we sometimes think we have to "explain" something more with quantum theory than there is contained in it, but that's pretty misleading.
Interesting Hardy is the one that got me into the probabilistic view of QM foundations.
Do you know if he has moved away from that?
Thanks
BillHardy revised his original (2001) set of axioms "replacing the simplicity axiom with more a compelling axiom" in 2011 (https://arxiv.org/abs/1104.2066). Per Hardy, "We show that classical probability theory and quantum theory are the only two theories consistent with the following set of postulates." His new postulates are Sharpness, Information Locality, Tomographic Locality, Permutability, and Sturdiness, which follow from two simple axioms:
Axiom 1 Operations correspond to operators.
Axiom 2 Every complete set of physical operators corresponds to a complete set of operations.
In the original version of our paper (as presented in the IJQF workshop last month), we advocated "quantum-classical contextuality," where physical reality isn't "quantum rather than classical, but fundamentally both." Thus, we made explicit reference to Hardy's 2011 statement and postulates. We nixed that when we decided to submit the paper to a physics journal.
Be forewarned about our book — as a mathematician, you'll want to avoid the philosophical threads. The main thread is probably already too philosophical for you :-)
he was the one who asked us to bring our adynamical approach to bear on his question "Why the Tsirelson bound?" when we gave a talk on our book at his QIT seminar last April.Have ordered a copy from Amazon.
Looking forward to reading it.
Interesting Hardy is the one that got me into the probabilistic view of QM foundations.
Do you know if he has moved away from that?
Thanks
Bill
What the quantum probabilities do instead is the following:
I understand that you can't have perfect cancellation if the axes ##vec{A}## and ##vec{B}## are not aligned. But why ask for cancellation (on the average) along axis ##vec{B}##?To fill in the blanks (not for you, I know you get it, but for others who might not have followed our exchange), rewrite ##frac{1}{2} (P_1 (vec{A} + vec{B}) + P_2 (vec{A} – vec{B}))cdotvec{B}## as ##frac{1}{2} ((P_1 + P_2)vec{A} + (P_1 – P_2)vec{B}))cdotvec{B} = frac{1}{2} (vec{A} + (P_1 – P_2)vec{B}))cdotvec{B}## where ##frac{1}{2}## is the magnitude of Alice's measurement along ##vec{A}## (note that both ##vec{A}## and ##vec{B}## are unit vectors). Now we're only considering those outcomes for which Alice measured ##+frac{1}{2}## (first bullet point), so the average value Alice would expect to measure along ##vec{B}## for her ##+frac{1}{2}## outcomes along ##vec{A}## is ##+frac{1}{2}vec{A}cdotvec{B} = +frac{1}{2}cos(theta)##. Since we need ##vec{L}## conserved to zero on average, we need Bob's average result along ##vec{B}## to cancel this ##+frac{1}{2}cos(theta)##. His average is ##+frac{1}{2}P_1 + -frac{1}{2}P_2 = (+frac{1}{2}P_1vec{B} + -frac{1}{2}P_2vec{B})cdotvec{B}##. Thus, we need ##+frac{1}{2}cos(theta) + frac{1}{2}P_1 + -frac{1}{2}P_2 = frac{1}{2} (vec{A} + (P_1 – P_2)vec{B}))cdotvec{B} = 0##. Again, you can divide up the results the same way for Bob and demand that Alice's average outcomes cancel his ##+frac{1}{2}cos(theta)## to derive the same quantum correlations.
I'm trying to get an intuitive understanding of the way that EPR probabilities (for anti-correlated spin-1/2 particles) are in some sense the closest we can get to the criteria:
… Those are the quantum probabilities for anti-correlated spin-1/2 particles.
That's sort of interesting, but my understanding of the motivation is a little muddled. I understand that you can't have perfect cancellation if the axes ##vec{A}## and ##vec{B}## are not aligned. But why ask for cancellation (on the average) along axis ##vec{B}##?You've arrived at the heart of the spin singlet state (uniquely producing the max deviation from the CHSH-Bell inequality, i.e., the Tsirelson bound). There is nothing special about axis ##vec{B}##, indeed you could have done the analysis looking at Bob's results along axis ##vec{B}## and required projection along axis ##vec{A}## to be zero in producing the correlation ##langle a,b rangle## . So, in which direction is angular momentum for the quantum exchange of momentum actually being conserved? It's being conserved on average from either Bob or Alice's perspective, i.e., along either ##vec{B}## or ##vec{A}##. In classical physics there is a definite direction for angular momentum ##vec{L}##, so with Alice and Bob measuring along random directions in the classical case we would expect neither ##vec{A}## nor ##vec{B}## to align with ##vec{L}##. Consequently, in the classical case, Alice and Bob should always (essentially) be measuring something less than the magnitude L of the conserved quantity ##vec{L}## (as shown in the picture of the SG experiment in the Insight). But, in the quantum case, it's as if there is no ##vec{L}## independent of Alice and Bob's measurements. That is, you can't account for the quantum correlation using a hidden variable or Mermin "instruction sets" on a trial-by-trial basis (giving classical correlations satisfying the Bell inequality). No, the bottom line is that the quantum correlation satisfies a truly frame-independent conservation principle.
As I said in the Insight, this is reminiscent of another frame-independent principle, the light postulate of SR. That postulate also led to "weird consequences," e.g., length contraction, time dilation, and relativity of simultaneity, and it was also opposed because it was something postulated not explained. Making this reference to the light postulate was motivated by quotes from Hardy and other reconstructionists in QIT. You read in many places in the QIT literature things like this Hardy quote The standard axioms of QT [quantum theory] are rather ad hoc. Where does this structure come from? Can we write down natural axioms, principles, laws, or postulates from which [we] can derive this structure? Compare with the Lorentz transformations and Einstein's two postulates for special relativity. Or compare with Kepler's Laws and Newton's Laws. The standard axioms of quantum theory look rather ad hoc like the Lorentz transformations or Kepler's laws. Can we find a natural set of postulates for quantum theory that are akin to Einstein's or Newton's laws? So, in our paper we point out that this explanation of the Tsirelson bound should satisfy the desideratum of QIT.
We're still waiting for Bub's response, he was the one who asked us to bring our adynamical approach to bear on his question "Why the Tsirelson bound?" when we gave a talk on our book at his QIT seminar last April. He wrote a nice blurb for that book, so we're hoping he now sees the relevance of adynamical/constraint-based explanation for QIT.
Any suggestions for where to submit the paper? I was thinking PRA, since they do QIT stuff.
I'm trying to get an intuitive understanding of the way that EPR probabilities (for anti-correlated spin-1/2 particles) are in some sense the closest we can get to the criteria:
If Alice measures her particle's spin along axis ##A## and Bob measures his particle's spin along axis ##B##, then it is impossible to satisfy both criteria, because unless ##A## and ##B## are aligned, none of the following combinations adds up to zero:
What the quantum probabilities do instead is the following:
This uniquely determines the probabilities ##P_1## and ##P_2##:
The latter equation becomes:
##frac{1}{2} (P_1 (cos(theta) + 1) + P_2 (cos(theta) – 1)) = 0## (where ##theta## is the angle between ##A## and ##B##)
These equations have the unique solution: ##P_1 = frac{1}{2} (1-cos(theta)) = sin^2(frac{theta}{2})##, ##P_2 = frac{1}{2} (1+cos(theta)) = cos^2(frac{theta}{2})##
Those are the quantum probabilities for anti-correlated spin-1/2 particles.
That's sort of interesting, but my understanding of the motivation is a little muddled. I understand that you can't have perfect cancellation if the axes ##vec{A}## and ##vec{B}## are not aligned. But why ask for cancellation (on the average) along axis ##vec{B}##?
Very nice post/paper
My thoughts on the matter have tended to be more along the lines of generalized probability models and QM being the simplest one after ordinary probability theory that allows continuous transformations between pure states. But it is quite abstract – yours is much more physical.
Very thought provoking.
Thanks
Bill
So the quantum weirdness in an EPR-type experiment is due to a combination of two things, neither of which is weird in itself:
But it seems that there is something else going on in EPR, which is a collapse-like assumption: When you measure a fermion's spin along some axis ##vec{a}##, then it is as if, afterward, it is definitely in that direction. That's different from an imagined classical measurement that is somehow constrained to give a discrete result. You could imagine (this is Bell's toy model) that the electron as an associated spin vector, ##vec{s}##, and measuring spin with respect to an axis ##vec{a}## would return ##+1/2## if the angle between ##vec{s}## and ##vec{a}## is less than 90[SUP]o[/SUP], and ##-1/2## otherwise. This would give a discrete result, but the result would not be the actual spin vector of the electron.Thnx for your comments, stevendaryl. 1 and 2 are spot on, but the collapse of some definite vector in that fashion doesn’t reproduce the quantum correlations (see the example in the Dehlinger paper referenced therein). The quantum correlations assume +1 or -1 is the “magnitude” and either Alice or Bob can claim they are always measuring the magnitude in each trial, it’s the other person who is getting the average, no collapse necessary. How can you not be impressed with such perspectival invariance?
So the quantum weirdness in an EPR-type experiment is due to a combination of two things, neither of which is weird in itself:
But it seems that there is something else going on in EPR, which is a collapse-like assumption: When you measure a fermion's spin along some axis ##vec{a}##, then it is as if, afterward, it is definitely in that direction. That's different from an imagined classical measurement that is somehow constrained to give a discrete result. You could imagine (this is Bell's toy model) that the electron as an associated spin vector, ##vec{s}##, and measuring spin with respect to an axis ##vec{a}## would return ##+1/2## if the angle between ##vec{s}## and ##vec{a}## is less than 90[SUP]o[/SUP], and ##-1/2## otherwise. This would give a discrete result, but the result would not be the actual spin vector of the electron.