- #1
zenterix
- 423
- 60
- TL;DR Summary
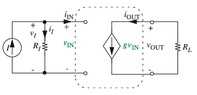
- In the shown depictions of a dependent source there is an input side and an output side. How exactly are they connected?
The amount of voltage provided by an independent voltage source and the amount of current provided by an independent current source do not depend on the circuit they are in.
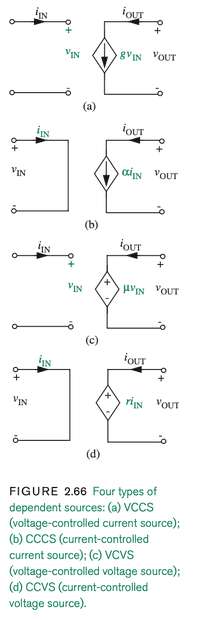
There are other types of sources, however, that do depend on the circuit they are in. That is, such dependent sources depend on (ie, are controlled by) other parameters in the circuit.
Here are depictions of four types of dependent sources
To summarize my question: how is the left side connected to the right side in practice?
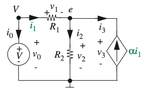
For example, consider the following circuit containing a current controlled current source (case b above)
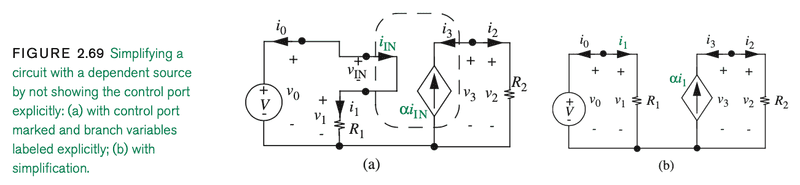
How exactly is it that the depicted input port affects the dependent current source?
I see that there is a connection in the center bottom. Is the connection between the input side and output side as simple as this or is the depiction somehow simplified?
It seems there must be some other connection. As far as I can tell, basic circuit analysis would predict no current in the bottom connection part.
There are other types of sources, however, that do depend on the circuit they are in. That is, such dependent sources depend on (ie, are controlled by) other parameters in the circuit.
Here are depictions of four types of dependent sources
To summarize my question: how is the left side connected to the right side in practice?
For example, consider the following circuit containing a current controlled current source (case b above)
How exactly is it that the depicted input port affects the dependent current source?
I see that there is a connection in the center bottom. Is the connection between the input side and output side as simple as this or is the depiction somehow simplified?
It seems there must be some other connection. As far as I can tell, basic circuit analysis would predict no current in the bottom connection part.