- #1
DaveC426913
Gold Member
- 22,436
- 6,106
Thinking last night about what I should expect see of the Toronto skyline, which is 40 miles across the lake from me.
Starting with an ideal scenario (nape-of-shore to nape-of-shore), a chord calculator tells me that for r=3900 mi. d=40 mi. the chord height will be 270 ft.
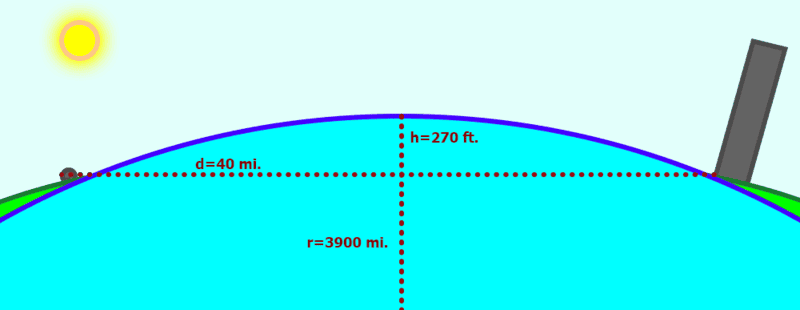
I was surprised at that height, and doubted my calculations. A 270 foot mountain in the middle of the lake is a lot! But I soon realized that it's not really a lot over 40 miles. It's rise-over-run of only 1:780.
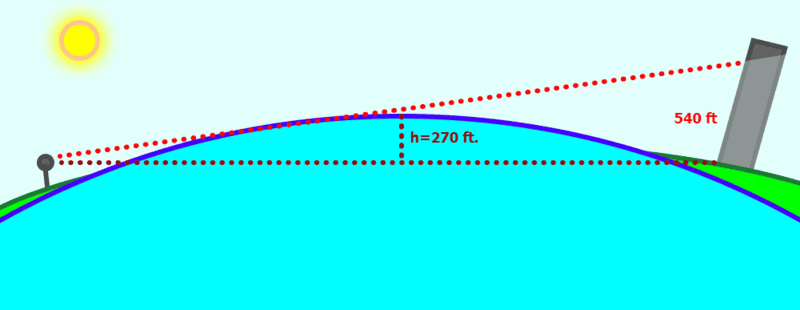
At first I assumed everything below that 270 foot mountain would be obscured, so I would only be able to see buildings from the 28th floor and up (assuming they are at the waterline). But upon reflection, I think I won't be able to see anything below double that, or 540 feet.
Confounding Factors:
Are my assumptions and calculations correct?
(Apologies for my wanton mixing of SI and metric)
Starting with an ideal scenario (nape-of-shore to nape-of-shore), a chord calculator tells me that for r=3900 mi. d=40 mi. the chord height will be 270 ft.
I was surprised at that height, and doubted my calculations. A 270 foot mountain in the middle of the lake is a lot! But I soon realized that it's not really a lot over 40 miles. It's rise-over-run of only 1:780.
At first I assumed everything below that 270 foot mountain would be obscured, so I would only be able to see buildings from the 28th floor and up (assuming they are at the waterline). But upon reflection, I think I won't be able to see anything below double that, or 540 feet.
Confounding Factors:
- I don't think my height above the water will make a difference if it's small enough. I mean, if my sightline is 10 feet above the waterline, that'll mean I can see down to 530 feet instead of 540 feet, right?
- I also have to remember that the visible buildings are many metres above the waterline, so I can't just count building stories to estimate altitude.
- And I'll have to time the observations right, when atmospheric refraction is at a minimum.
Are my assumptions and calculations correct?
(Apologies for my wanton mixing of SI and metric)
Last edited:

